H. Má Einsteinova teória nejaké využitie aj v bežnom živote?
Global Positioning System — GPS
(riešená úloha)

OBSAH:

S efektom vplyvu gravitačného poľa a rýchlosti pohybu na plynutie času sa museli vyrovnať aj vedci, ktorí projektovali Global Positioning System - GPS (Globálny systém na určovanie polohy). Dnes má tento systém okrem pôvodného vojenského využitia aj bohaté civilné využitie. Prijímače GPS sa montujú do automobilov, turisti si ich berú so sebou na túry, sú nimi vybavené lietadlá a lode, používajú sa na výrobu máp a na záchranu stroskotancov.

Systém pracuje pozoruhodne jednoducho. Pozostáva z 24 družíc obiehajúcich okolo Zeme po kruhových obežných dráhach s periódami približne 12 hodín, ktoré sú rozmiestnené v šiestich rovnomerne rozložených obežných rovinách. Každá z družíc má na palube štvoro atómových hodín a vysiela časové signály smerom k Zemi. Hodiny všetkých družíc sú navzájom zosynchronizované. Prijímač so zabudovaným mikroprocesorom na zemskom povrchu analyzuje signál z aspoň štyroch rôznych družíc a zobrazí informáciu o svojej polohe (zemepisná šírka, zemepisná dĺžka a nadmorská výška). Bežné civilné prijímače majú veľkosť kalkulačky, dajú sa kúpiť už za sto dolárov a určujú polohu s presnosťou na približne 100 metrov. Vojenské verzie dosahujú presnosť desiatok metrov.

Signál, ktorý vysiela každá družica má v sebe zakódovanú informáciu o čase na atómových hodinách družice a o jej polohe. Hodiny na prijímači zaznamenajú svojimi hodinami čas prijatia každého signálu. Prijímač vypočíta rozdiel časov medzi vyslaním a prijatím signálu a z tohto rozdielu vypočíta vzdialenosť, ktorú (rýchlosťou svetla) signál preletel. Tým pádom zistí, ako ďaleko sa nachádzal od vysielača, keď bol vyslaný signál.

Ak by sme chceli určiť kde sa v priestore nachádza prijímač, potrebovali by sme poznať jeho vzdialenosť od aspoň troch družíc. Má to však jeden háčik. Hodiny na prijímači nie sú atómové t.j. sú omnoho nepresnejšie ako hodiny na družiciach. Preto je nutné, aby prijímač prijímal ešte dodatočný signál z ďalšej - štvrtej - družice, ktorý umožňuje prijímaču spracúvať ostatné signály tak, akoby obsahoval atómové hodiny.

Ako vedia jednotlivé družice systému, aká je ich poloha? Ministerstvo obrany neustále monitoruje presnú polohu a rýchlosť všetkých družíc. Táto informácia je vysielaná späť na družice, ktoré ju vysielajú spolu s časovými signálmi.

Na to, aby prijímač správne určil svoju polohu, musí vziať do úvahy vplyv gravitačného poľa a rýchlosti družíc na beh času na atómových hodinách na družiciach. Dá sa vypočítať, že hodiny na družiciach a hodiny na Zemi by sa po uplynutí 1 dňa rozbehli o 39 000 nanosekúnd. Svetlo za takýto čas prejde vzdialenosť asi 12 km. Až taká by mohla byť chyba, ktorej by sa GPS mohol dopustiť, keby nebola do úvahy braná teória relativity!

Skúste zovšeobecniť úvahy z tejto a predchádzajúcej stránky a použiť ich na porovnanie tempa tikania dvojice hodín nachádzajúcich sa v radiálnom gravitačnom poli Zeme. Predpokladajte, že hodiny vysielača sa nachádzajú na družici, obiehajúcej v rovine rovníka po kružnicovej orbite s periódou 12 hodín a hodiny prijímača sa nachádzajú na rovníku na povrchu Zeme. O koľko nanosekúnd sa hodiny rozbehnú, keď na povrchu Zeme uplynie čas 1 deň? Potrebné údaje si nájdite v tabuľkách! Podarilo sa vám overiť údaje z textu?

Riešenie

Potrebujeme porovnať tempo tikania hodín na družici, ktorá sa nachádza vo vzdialenosti r od stredu Zeme a má rýchlosť v a na hodinách, ktoré sa nachádzajú na zemskom povrchu vo vzdialenosti R_Z od stredu Zeme a majú vzhľadom na stred rýchlosť v_Z.

Problém vyriešime v dvoch krokoch. Najprv budeme predpokladať, že rýchlosti oboch hodín sú nulové. Potom, v druhom kroku, sa pozrieme, čo sa stane, keď budú mať rýchlosti.

Takže predpokladajme, že hodiny sa nehýbu. Hodiny družice nech sú priamo nad hodinami na zemskom povrchu. Ako porovnať tempá ich tikania? Podobne, ako v časti B, keď sme porovnávali tempá hodín Veroniky a Tomáša. Rozdiel je len v tom, že tentoraz sa hodiny nachádzajú v radiálnom gravitačnom poli, ktoré má v rôznych bodoch priestoru rôznu intenzitu. Gravitačné pole s výškou slabne, preto bude pri horných hodinách slabšie ako pri dolných. Gravitačné zrýchlenie je dané vzťahom

kde G = 6,67.10^–11m³.s^–2.kg^–1 je gravitačná konštanta, M_Z = 5,98.10²⁴ kg, je hmotnosť Zeme, r je vzdialenosť od stredu Zeme.

Predtým sme nechali Veroniku pustiť svoje hodiny, ktoré vysielali signály. Keď dorazil prvý signál k spodným Tomášovým hodinám, pustil svoje hodiny aj Tomáš. Tým sa problém porovnania rýchlosti plynutia času v rôznych miestach v gravitačnom poli zmenil na problém porovnania rýchlosti plynutia času v dvoch inerciálnych sústavách. Pole, v ktorom sa nachádzali Tomáš a Veronika bolo homogénne.

V nehomogénnom poli nevystačíme s dvomi pomocnými inerciálnymi sústavami. Budeme ich potrebovať veľmi veľa! Predstavme si, že medzi Veronikou, ktorá je pri hodinách na družici, a Tomášom, ktorý je pri hodinách na Zemi, sa nachádza rovnomerne rozmiestnených n–1 ďalších pozorovateľov. Ich počet zvolíme tak, aby ich vzdialenosti Dr boli menšie ako 100 metrov. Na vzdialenosť 100 metrov možno gravitačné pole Zeme považovať za homogénne. Každý pozorovateľ má tričko a na ňom má veľkými písmenami napísané svoje poradové číslo. Pozorovateľ hneď nad Tomášom má číslo 1 a pozorovateľ hneď pod Veronikou má teraz číslo n–1. Vzdialenosť medzi Veronikou a Tomášom tak bola rozdelená na n rovnakých úsekov, pričom veľkosť gravitačného zrýchlenia na n-tom úseku je

pričom r_n predstavuje vzdialenosť od stredu Zeme k stredu úseku.

Veronika si môže porovnať tempo tikania svojich hodín s tempom tikania Tomášových hodín prostredníctvom pozorovateľov medzi nimi. Najprv si porovná tempo tikania s pozorovateľom tesne pod ňou. Ten zaregistruje, že jej hodiny tikajú s frekvenciou

Prečo sme použili vzorec, ktorý sme predtým odvodili pre homogénne gravitačné pole? Preto, lebo Veronika a pozorovateľ tesne pod ňou sú tak blízko, že pole sa medzi nimi dá považovať za homogénne.

Pozorovateľ tesne pod Veronikou si nastaví tempo tikania svojich hodín na frekvenciu f_n–1 Veronikiných hodín a porovná si rovnakým spôsobom nové tempo tikania svojich hodín so susedom pod sebou. Ten zaregistruje frekvenciu tikania

Nastaví svoje hodiny tak, aby tikali touto frekvenciou a porovná si ich so susedom pod sebou.

Tak to bude pokračovať, až pokým si pozorovateľ tesne nad Tomášom, neporovná svoje hodiny s Tomášom. Tomáš nameria frekvenciu tikania hodín pozorovateľa 1 danú vzťahom

Nastaví si podľa nej svoje hodiny. Tak Tomáš dosiahne, že jeho hodiny budú tikať rovnako ako Veronikine.

Ako však vypočítame rýchlosť ich tikania? Stačí pospájať všetky doterajšie vzťahy. Platí:

Teraz môžeme všetky zátvorky vynásobiť a keďže všetky členy v zátvorkách za jedničkami sú oproti jedničkám veľmi malé, zanedbať všetky členy súčinu vyššieho ako prvého rádu. Dostaneme:

Súčet za jednotkou v zátvorke sa v limite pre blíži k integrálu , ktorý je úmerný gravitačnému potenciálu Veroniky vzhľadom k nulovej hladine na povrchu Zeme.

To nám umožňuje zovšeobecniť vzťah medzi frekvenciou dvoch rôznych hodín v rôznych miestach ľubovoľného slabého gravitačného poľa:

kde je rozdiel gravitačných potenciálov horných a dolných hodín.

Vráťme sa späť k nášmu príkladu. Integrál, ktorý sme získali je možné ľahko vypočítať. Dostaneme:

Preto Tomáš zistí, že Veronikin čas plynie frekvenciou

Prvý krok riešenia nášho problému už máme za sebou. Teraz k druhému kroku: Uvážime, že družica sa pohybuje rýchlosťou v a hodiny na povrchu rýchlosťou v_Z.

Znovu použijeme Tomáša a Veroniku. Budeme predpokladať, že sa nachádzajú v pokoji vzhľadom na stred Zeme. Tesne vedľa Veroniky práve prelieta družica a tesne vedľa Tomáša práve letia (spolu s povrchom Zeme) hodiny na povrchu. Označme teraz frekvenciu tikania Veronikiných hodín f_0V a frekvenciu tikania Tomášových hodín f_T. Posledný vzťah (vzťah medzi týmito frekvenciami) môžeme potom v novom označení zapísať ako

Ak teraz hodiny na družici tikajú v sústave družice s frekvenciou f₀, budú v sústave Veroniky tikať s nižšou frekvenciou . Veronika si na túto frekvenciu nastaví svoje hodiny. Tým pádom si bude musieť aj Tomáš nastaviť svoje hodiny na novú frekvenciu tikania, konkrétne na frekvenciu

Tomáš túto frekvenciu interpretuje ako frekvenciu tikania hodín na družici.

Vzhľadom na Tomáša sa hodiny na Zemi pohybujú rýchlosťou v_Z. Tomáš bude pozorovať, že ich frekvencia f_Z je

Tomáš teraz môže frekvencie tikania oboch hodín (na Zemi a na družici) porovnať. Dostane

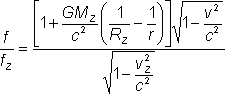
Použitím približných vzorcov možno tento vzťah upraviť na

Zrejme , kde

Keď tento vzťah vynásobíme dĺžkou jedného dňa na Zemi t_Z, dostaneme vzťah pre dodatočný počet DN tiknutí horných hodín

Z tohto vzťahu už nie je ťažké vypočítať, že za 1 deň uplynie na družici zhruba o 39 000 nanosekúnd viac ako na Zemi. Treba na to len zistiť veličiny r, v a v_Z. To už iste zvládnete sami, veď je to záležitosť fyziky prvého ročníka!