
F. Druhý Newtonov zákon
OBSAH:
ÚvodA.
Einsteinova teória gravitácie
B.
Gravitácia a čas
C.
Princíp najmenšieho účinku
D.
Účinok na priamom úseku svetočiary
E.
Hľadanie svetočiary jablka
F.
Druhý Newtonov zákon
G.
Zákon zachovania mechanickej energie
H.
Bonus: Má Einsteinova teória nejaké využitie aj v bežnom živote?
Global Positioning System — GPS
I.
Odkazy
Z princípu najmenšieho účinku, ktorý sme získali ako dôsledok Einsteinovej teórie gravitácie, aplikovanej na slabé gravitačné pole v okolí povrchu Zeme, môžeme teraz ľahko odvodiť Newtonov druhý pohybový zákon pre pohyb jablka. To znamená, že Newtonov zákon pre nás prestáva byť najhlbším vysvetlením pohybu. Namiesto toho sa ním stáva VTR.
|
Čo znamená "vysvetliť" (Daniel F. Styer v knihe Zvláštny svet kvantovej mechaniky) Koniec koncov, čo znamená "vysvetliť"? Pripusťme, že sa ma spýtate: "Prečo včera pršalo?" Mojou odpoveďou by mohlo byť: "Pretože nás zasiahol studený front." Potom by ste mohli položiť otázku: "Ale prečo nás zasiahol studený front?" Odpovedal by som "Pretože ho sem postrčilo prúdenie vzduchu." Vy na to: "Nuž ale, prečo ho sem prúdiaci vzduch postrčil?" Ja: "Pretože Slnko ohrialo Saskatchewan, a tým vychýlilo vzdušný prúd." (Každý, kto niekedy vychovával dieťa, pozná tieto nikdy nekončiace otázky až príliš dobre.) Vy: "Dobre, ale prečo Slnko ohrieva objekty?" Na tejto úrovni na vašu otázku naozaj neviem odpovedať. Viem, že slnečné lúče prenášajú energiu (čo viete aj vy), a veda dokáže opísať tento transport energie so skvelou presnosťou. Lenže veda nevie vysvetliť tento transport energie alebo povedať prečo sa to deje. Táto ukážka ilustruje fakt, že "vysvetliť" znamená "vysvetliť pomocou niečoho fundamentálnejšieho". V určitom okamihu hocijaký reťazec otázok prejde k najfundamentálnejším témam a predstavám a tu nutne končí. V tejto chvíli najfundamentálnejšie myšlienky vo fyzike nazývame "kvantová elektrodynamika" a "kvantová chromodynamika" [v prípade gravitácie ich nazývame "všeobecná teória relativity"]*, . . . Možno jedného dňa budeme mať ešte fundamentálnejšie pojmy a myšlienky, také že na otázky "prečo" súvisiace s kvantovou elektrodynamikou [alebo v prípade gravitácie týkajúce sa všeobecnej teórie relativity] bude možné odpovedať pomocou týchto nových myšlienok. Na druhej strane, otázky "prečo" vzťahujúce sa k týmto fundamentálnejším veciam budú opäť nezodpovedateľné! Skrátka, na konci ľubovolnej reťaze otázok, ktoré prechádzajúcu čoraz hlbšie a hlbšie, vie veda dať len popis (fakty), ale nie vysvetlenie (zdôvodnenie pre tieto fakty). * Komentáre v [ ] boli k originálu pridané. |
Uvažujme priestoročasový diagram pre pohyb nášho jablka. Porušíme v tomto prípade zaužívané označenie osí známe zo špeciálnej teórie relativity a označíme vodorovnú os ako os t a zvislú os ako os h. Pomôže to lepšie našej predstavivosti, keďže jablko letí do výšky.
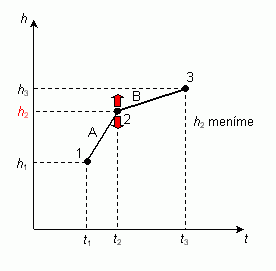
Uvažujme v tomto diagrame krátky úsek svetočiary jablka 1-2-3 zložený z dvoch priamych, veľmi krátkych úsekov A a B. Krajnými bodmi úsekov sú udalosti 1[t1, h1], 2[t2, h2], 3[t3, h3]. Predpokladajme, že udalosti 1 a 3 sú dané pevne. Pevne je daný aj čas udalosti 2. Poloha h2 udalosti 2, nie je daná pevne. Môžeme je meniť. Pritom, ako ju budeme meniť budeme hľadať takú jej polohu, pri ktorej je účinok na svetočiare 1-2-3 najmenší.
Účinok na celej svetočiare 1-2-3 získame ako súčet účinku na svetočiare 1-2 a účinku na svetočiare 2-3, teda ako
Po dosadení vzťahov pre účinky na priamych úsekoch 1-2 a 2-3 pre celkový účinok dostaneme
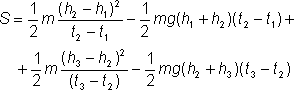
Keďže je všetko okrem výšky h2 pevne dané, je účinok S iba funkciou h2. Naším cieľom je zistiť, čo musí platiť, aby bol účinok minimálny. Z matematiky vieme, že to nastane vtedy, keď bude derivácia účinku podľa h2 rovná nule:
Ak zderivujeme vzťah pre účinok a mierne výsledok upravíme, dostaneme:
Preusporiadame členy a znovu mierne upravíme:
Výraz v zátvorke na pravej strane predstavuje rozdiel rýchlostí na úsekoch B a A. Výraz v zátvorke na ľavej strane predstavuje súčet polovíc časových dĺžok úsekov A a B. Je to vlastne čas, za ktorý sa stihla rýchlosť zmeniť z rýchlosti vA na rýchlosť vB, prípadne ešte inak: Je to časová vzdialenosť stredov intervalov A a B.
Rovnicu teda možno zapísať v tvare:
alebo ešte krajšie:
Táto rovnica je vyjadrením druhého Newtonovho pohybového zákona pre pohyb jablka v tiažovom poli Zeme.
To, čo sme práve ukázali, platí pre lomenú svetočiaru 1-2-3. Mohli by sme zobrať ďalšie udalosti cez ktoré jablko prechádza, napríklad udalosti 4, 5, ... Rovnaký postup môžeme použiť aj na lomenú svetočiaru 2-3-4, prípadne svetočiaru 3-4-5. Dôjdeme k tomu, že pre všetky takéto lomené dvojúsekové svetočiary musí platiť Newtonov pohybový zákon. Musí teda platiť pre celú, ľubovoľne dlhú svetočiaru, spájajúcu začiatočnú a koncovú udalosť.
Overenie konštantnosti zrýchlenia na pravej trajektórii
Nasledujúci Java applet vám ponúka možnosť overiť, že pri tej pravej trajektórii jablka je zrýchlenie prislúchajúce každej dvojici priamych úsekov svetočiary jablka konštantné, teda že pohyb jablka sa naozaj riadi druhým Newtonovým zákonom.
Zrýchlenia na jednotlivých dvojiciach úsekov súvisia s aktuálnou vybratou svetočiarou a sú zobrazené na pravej strane appletu. Ťuknite myšou do appletu. Tým spustíte hľadanie optimálnej svetočiary s najmenším účinkom. Keď sa už účinok nebude meniť, znovu kliknite do appletu. Hľadanie sa zastaví. Skúste potom myšou meniť polohy jednotlivých bodov svetočiary a všimnite si, čo sa pritom deje so zrýchlením. Prečo sa vychýlením jedného bodu zmenia v tabuľke až tri hodnoty zrýchlenia?