B. Gravitácia a čas

OBSAH:

Veľmi zaujímavým dôsledkom Einsteinovej teórie gravitácie je fakt, že čas plynie v gravitačnom poli v rôznych výškach rôzne rýchlo. Dokážeme to pomocou zaujímavého myšlienkového experimentu.

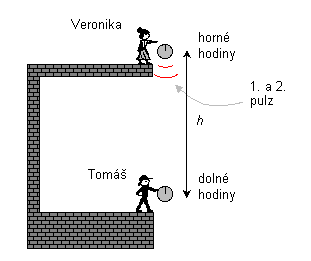
Predstavme si, že máme dvoje identické hodiny. Jedny sa nachádzajú pri povrchu Zeme a druhé vo výške h nad povrchom Zeme, nad prvými hodinami. Pri spodných hodinách sedí pozorovateľ Tomáš a pri horných hodinách je jeho kamarátka Veronika. Každé z hodín tikajú s frekvenciou f₀. To znamená, že každú sekundu ich času tiknú f₀ krát. Pri každom tiknutí vysielajú horné hodiny veľmi krátky záblesk svetla.

V istom okamihu vyšlú horné hodiny prvý záblesk svetla a Veronika ich v tom istom okamihu uvoľní, aby mohli voľne padať. Tesne po uvoľnení majú zanedbateľnú rýchlosť, takže stále prakticky merajú Veronikin čas vo výške h. Vtedy vyšlú druhý záblesk. Ďalej padajú a neustále rýchlo vysielajú záblesky svetla. Tretí, štvrtý, atď.

V okamihu, keď dorazí prvý záblesk svetla k spodným hodinám, Tomáš ich uvoľní. Začnú padať do šachty, vykopanej v zemi. Tesne po zachytení prvého záblesku sa spodné hodiny pohybujú voči zemi zanedbateľnou rýchlosťou a preto merajú stále prakticky Tomášov čas pri povrchu Zeme.

Naším cieľom bude porovnať tempá (frekvencie) tikania horných a dolných hodín. Práve kvôli tomu účelu vysielajú horné hodiny pulzy svetla k spodným hodinám. Všimneme si prvé dva pulzy. Z horných hodín boli vyslané tak rýchlo za sebou, že sa medzi ich vyslaním nestačili horné hodiny prakticky pohnúť. Sú stále pri Veronike, vo výške h. Každý z pulzov musí prekonať rovnakú vzdialenosť v gravitačnom poli, aby sa dostal dole k Tomášovi. Každému pulzu potrvá cesta dole rovnaký čas. Čas, ktorý nameria Tomáš medzi príletmi oboch pulzov, bude preto považovať za dobu medzi tiknutiami Veronikiných hodín. Tento čas medzi tiknutiami zistí na svojich hodinách, ktoré pustil, keď dorazil prvý pulz svetla, a ktoré sú stále ešte prakticky v pokoji.

Problém porovnania rýchlosti plynutia času v dvoch rôznych výškach v gravitačnom poli sme takto previedli na problém porovnania času medzi vyslaním dvoch impulzov a času medzi ich prijatím v dvoch rôznych voľne padajúcich vzťažných sústavách, ktoré sa riadia zákonmi, aké by boli vo vesmíre bez gravitácie.

Zhrňme teda, čo vieme:

1. Máme dvoje padajúce hodiny, Veronikine a Tomášove. Veronikine hodiny bežia tak rýchlo, ako plynie čas pri Veronike a Tomášove hodiny bežia tak rýchlo, ako rýchlo plynie čas dole pri Tomášovi. (Veronikine hodiny tiknú f₀ krát za Veronikinu sekundu a Tomášove tiknú f₀ krát za Tomášovu sekundu.) Keďže oboje hodiny padajú, nebude sa rýchlosť behu hodín v ďalších časových okamihoch nijako meniť, lebo ich vzťažné sústavy sú podľa princípu ekvivalencie na nerozoznanie od inerciálnych.
   
   
2. Veronikine hodiny vysielajú pulzy svetla f₀ krát za jej sekundu. Tieto pulzy sú zachytávané Tomášovými hodinami. Tomáš interpretuje frekvenciu prichádzajúcich pulzov (to koľko ich dorazí za jeho sekundu) ako rýchlosť plynutia Veronikinho času.

Všimnime si teraz jednu veľmi zaujímavú a podstatnú vec. Aká je vzájomná relatívna rýchlosť horných a spodných hodín? Keďže Tomáš vypustil svoje hodiny neskôr ako Veronika, budú vždy padať menšou rýchlosťou ako Veronikine hodiny. Jeho a jej hodiny sa budú pomaly približovať. To znamená, že spodné hodiny nebudú zachytávať záblesky od horných hodín s frekvenciou f₀, ale s väčšou frekvenciou f. Na vine je známy Dopplerov jav (Jednoduché odvodenie pre malé rýchlosti nájdete nižšie).

Tomáš preto usúdi, že Veronikin čas plynie rýchlejšie ako jeho. O koľko rýchlejšie?

Svetelný pulz dorazí od Veroniky k Tomášovi prakticky za čas , keďže je výška h pomerne malá a rýchlosť svetla je veľmi veľká. Tento čas je taký krátky, že nie je nutné uvažovať zmenu vzdialenosti medzi obidvoma hodinami, spôsobenú pádom horných hodín. Za ten čas nadobudnú Veronikine hodiny rýchlosť . Toto je rýchlosť, ktorou sa budú k sebe približovať obe sústavy padajúcich hodín. Keďže je táto rýchlosť malá, môžeme pri výpočte frekvencie f príjmu dopadajúcich pulzov použiť vzorec pre klasický Dopplerov jav:

Po dosadení za rýchlosť dostaneme, že

Ešte dve poznámky:

1. V našich úvahách sme používali Newtonovu teóriu gravitácie a jeho pohybové zákony, na to, aby sme odvodili efekt teórie relativity. Už sme vraveli, že slabé gravitačné polia možno veľmi dobre popísať aj Newtonovou teóriou, do ktorej Einsteinova hladko prechádza. Urobiť to je v našom prípade nutné, keďže sme sa zatiaľ nezoznámili podrobne s relativistickými gravitačnými zákonmi. Dôležité je, že sme dostali správne výsledky.
   
   


2. V našich úvahách používame napríklad vo vzorci v = gt čas t, bez toho, že by sme uvažovali, že čas plynie v rôznych výškach rôznou rýchlosťou. Môžeme si to dovoliť, lebo rozdiel v plynutí času je zanedbateľne malý a chyba, ktorej sme sa dopustili je veľmi malá. Pokojne môžeme prehlásiť, že čas t je čas pri povrchu Zeme.

Dopplerov jav pre malé rýchlosti (odvodenie) Predpokladajme, že sprava prilieta v inerciálnej vzťažnej sústave laboratória konštantnou rýchlosťou v raketa. Raketa vysiela neustále záblesky (krátke pulzy) svetla. Medzi jednotlivými zábleskmi v sústave rakety uplynie čas Dt. Keďže je rýchlosť rakety voči laboratóriu malá, môžeme predpokladať, že skoro rovnaký čas uplynie medzi zábleskmi aj v sústave laboratória (zanedbávame dilatáciu času). 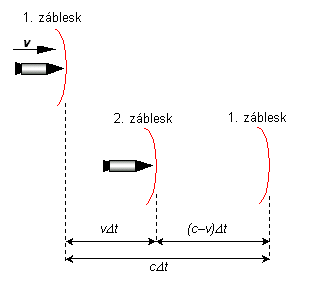Uvažujme dva za sebou idúce záblesky, záblesk 1 a 2. Bude nás zaujímať, v akom časovom odstupe Dtpoz dorazia do oka pozorovateľa, stojaceho napravo v laboratóriu. Z obrázka je vidieť, že medzi vyslaním prvého a druhého záblesku sa raketa posunie o vzdialenosť v Dt. Prvý záblesk za tento čas urazí vzdialenosť c Dt. Vzdialenosť medzi zábleskmi v sústave laboratória preto bude (c – v) Dt. Do oka pozorovateľa dorazia v časovom odstupe . Čo bude platiť pre frekvenciu dopadania zábleskov do oka pozorovateľa? Koľko ich dopadne za sekundu? Zrejme 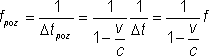. Využili sme pritom fakt, že frekvencia vysielania pulzov v rakete je . Ak uvážime, že rýchlosť rakety je malá, môžeme použiť približný vzorec a vzťah medzi frekvenciami upraviť na To je vzorec pre Dopplerov jav, ktorý sme použili v texte.