
D. Účinok na priamom úseku svetočiary
OBSAH:
ÚvodA.
Einsteinova teória gravitácie
B.
Gravitácia a čas
C.
Princíp najmenšieho účinku
D.
Účinok na priamom úseku svetočiary
E.
Hľadanie svetočiary jablka
F.
Druhý Newtonov zákon
G.
Zákon zachovania mechanickej energie
H.
Bonus: Má Einsteinova teória nejaké využitie aj v bežnom živote?
Global Positioning System — GPS
I.
Odkazy
Uvažujme priamy úsek svetočiary jablka, začínajúci v udalosti [t1, h1] a končiaci v udalosti [t2, h2]. Účinok prislúchajúci tomuto úseku svetočiary bude funkciou všetkých štyroch premenných t1, h1, t2, h2.
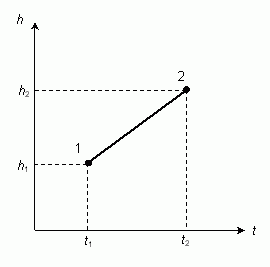
Keďže sa jablko medzi oboma udalosťami pohybuje po priamej svetočiare, má počas celého pohybu konštantnú rýchlosť
Podľa definície vypočítame účinok S ako
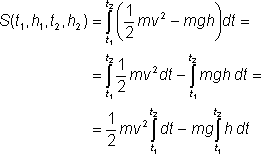
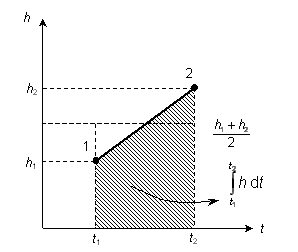
Pri predchádzajúcich úpravách sme využili, že integrál rozdielu dvoch funkcií je rozdielom ich integrálov. Vybrali sme pred integrály konštantné faktory. Zostáva nám vypočítať už len dva jednoduché integrály. Prvý z nich sa jednoducho rovná t2 – t1. Druhý z nich vypočítame pomocou grafu. Finta je v tom, že pri integrovaní stačí nahradiť lineárnu funkciu jej strednou hodnotou. V našom prípade
Ak tento výsledok dosadíme do vzťahu pre účinok a jednoducho upravíme, dostaneme výsledný vzťah pre účinok na priamom úseku svetočiary: