C. Princíp najmenšieho účinku

OBSAH:

Vráťme sa teraz k nášmu jablku. V istom mieste pri zemi v čase 0 sekúnd ho vyhodíme zvislo nahor a chceme aby bolo v neskoršom čase, dajme tomu v čase 10 sekúnd na tom istom mieste. Ako sa bude jablko pohybovať? Einstein nám hovorí, že tak, aby medzi týmito dvoma udalosťami čo najviac zostarlo. Keďže čas vo výške plynie rýchlejšie ako pri zemi, zostarne jablko najviac, keď strávi čo najviac času vo veľkých výškach. Na to, aby sa do veľkých výšok dostalo a stihlo sa vrátiť načas späť sa však musí pohybovať veľkými rýchlosťami. To znamená, že vstúpi do hry dilatácia času známa zo špeciálnej teórie relativity a plynutie času jablka spomalí. Jablko teda nesmie letieť príliš vysoko, lebo sa mu to neoplatí. Namiesto toho si nájde optimálnu trajektóriu v priestoročase (svetočiaru), na ktorej medzi danými dvoma udalosťami zostarne najviac.

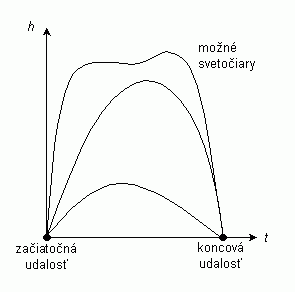
Ak hodiny spojené s jablkom majú frekvenciu tikania f₀ a rýchlosť v vzhľadom na zem, pričom sú v nulovej výške, tak v sústave zeme budeme registrovať, že ich plynutie času sa spomaľuje (dilatácia času) podľa vzťahu

Ak nebudú v nulovej výške, musíme uvážiť zrýchľovanie plynutia času spojené s výškou. Ak máme jablko vo výške h v gravitačnom poli zeme a jablko sa pohybuje rýchlosťou v, bude pozorovateľ na zemi pozorovať, že frekvencia tikania s jablkom spojených hodín je

Predpokladajme, že rýchlosť jablka je omnoho menšia ako rýchlosť svetla. Vtedy možno použitím približných vzorcov predchádzajúci vzťah upraviť do tvaru

Počet tiknutí hodín spojených s jablkom musí byť medzi začiatočnou a koncovou udalosťou maximálny. Počet tiknutí hodín N vypočítame ako:

kde t₁ = 0 s a t₂ = 10 s.

Po dosadení dostaneme:

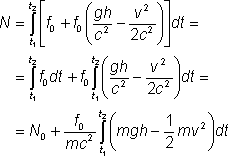
N₀ predstavuje počet tiknutí hodín jablka, keby bolo celý čas vo výške 0. K nemu treba podľa predchádzajúceho vzťahu pripočítať prírastok

.

Jablko sa bude pohybovať tak, aby bol tento prírastok maximálny. Spomínaný prírastok môžeme zapísať aj nasledujúcim spôsobom:

kde S je veličina

.

Kvôli znamienku mínus bude DN maximálne, keď bude veličina S minimálna. Veličine S sa hovorí účinok. Je to integrál rozdielu kinetickej a potenciálnej energie jablka pozdĺž jeho svetočiary.

Tomuto princípu sa hovorí princíp najmenšieho účinku. Ako sme videli, princíp najmenšieho účinku je priamym dôsledkom Einsteinovej teórie gravitácie. Pohyb jablka už máme v princípe popísaný. Pohybuje sa tak, aby bol účinok najmenší. No ako to je? Ako sa vlastne pohybuje? Kde presne sa nachádza v rôznych časoch?

Na to, aby sme na tieto otázky mohli odpovedať, musíme najprv vedieť, ako vypočítať účinok na ľubovoľnej svetočiare. To je dosť zložitá úloha. Zjednodušíme si ju však tým, že krivú svetočiaru nahradíme sériou krátkych priamych, za sebou idúcich úsekov. Ak budeme vedieť vypočítať účinok na jednom priamok úseku, budeme vedieť vypočítať aj účinok na celej svetočiare.