G. Algoritmus

OBSAH:

Naším cieľom na tejto stránke bude ozrejmiť si podrobne algoritmus na kreslenie Mandelbrotovej množiny a ukázať si jeho konkrétnu implementáciu v jazyku Java a v jazyku Delphi Pascal.

Z toho, čo bolo doteraz o Mandelbrotovej množine povedané, by malo byť jasné, že keď chceme nakresliť na počítači obrázok Mandelbrotovej množiny, musíme mu zadať hodnotu limit, ktorá bude udávať presnosť, s akou je Mandelbrotova množina nakreslená. Čím väčšia je hodnota premennej limit, tým detailnejší obrázok dostaneme, ale zrejme aj tým dlhší budeme potrebovať výpočtový čas.

Keď by sme mali stručne povedať, čo robí počítač, keď počíta obrázok Mandelbrotovej množiny, mohli by sme to povedať takto: Počítač prechádza jednotlivými bodmi c Gaussovej roviny a pre každý z nich počíta členy pomocnej postupnosti, pokým neprekročí jej prislúchajúca orbita hraničnú kružnicu, prípadne pokým nedosiahne počet vypočítaných členov maximálnu hodnotu limit. Počítač potom rozhodne, akú farbu priradí bodu c.

To, čo sme práve urobili, bolo to, že sme slovne popísali algoritmus na kreslenie Mandelbrotovej množiny. Najlepšie sa algoritmy chápu pomocou vývojových diagramov. Pod týmto odstavcom je vývojový diagram, pomocou ktorého by ste mohli postupovať, keby ste sa chceli zahrať na počítač, a mali nakresliť obrázok Mandelbrotovej množiny. Prečítajte si ho!

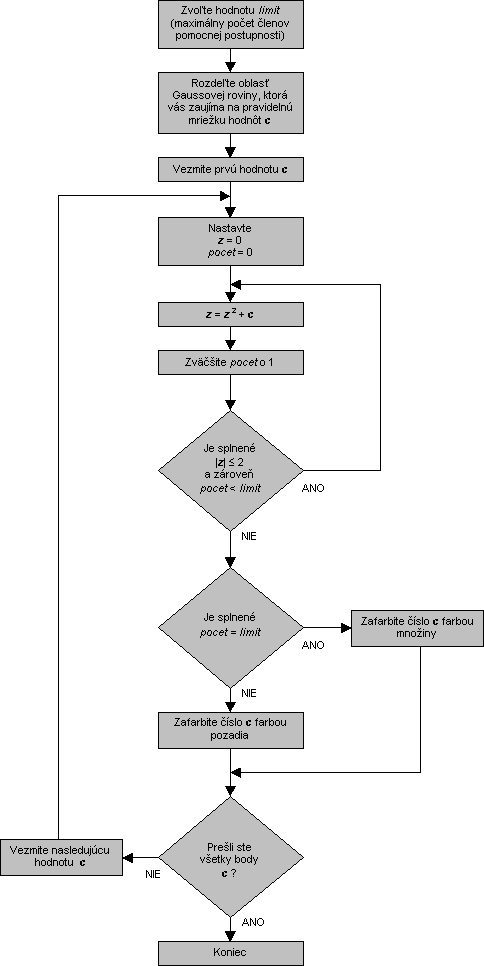
V tomto okamihu by vám už mali byť všetky hlavné myšlienky ohľadom kreslenia Mandelbrotovej množiny jasné. Zostáva nám už len ukázať, ako konkrétne by vyzeral prepis tohto algoritmu do konkrétnych jazykov. Vybrali sme si jazyk Java, lebo v ňom boli napísané všetky applety na týchto stránkach a tiež jazyk Pascal, lebo je rozšírený a mnohí sa ho učíte na hodinách programovania.

Tieto prepisy uvádzame len s krátkym komentárom. Keď viete programovať v týchto jazykoch, akýkoľvek komentár je zbytočný. Keď v nich programovať neviete, kľudne zvyšok stránky preskočte.

Tu je komentár: V oboch implementáciách je daná zobrazovacia plocha s veľkosťou 401 x 401 pixelov. Program prechádza v dvojnásobne vnorenom cykle for postupne cez všetky stĺpce a pre každý stĺpec cez všetky jeho riadky. Ku každému pixelu so súradnicami [i, j] vypočíta zodpovedajúce komplexné číslo c. Rozsah reálnych aj imaginárnych súradníc čísel c je od –2 do 2. Potom už program robí s číslom c to, čo je popísané vo vývojovom diagrame.

Tu je zodpovedajúca metóda na kreslenie množiny v JAVE:

public void kresliMnozinu(){
   int i,j,pocet,limit;
   double cr,ci,zr,zi,zr2,zi2;
   limit=256;
   for (i=0; i<401; i++)
     for (j=0; j<401; j++){
         cr=((float)(i-200))/((float)100);
         ci=((float)(200-j))/((float)100);
         zr=0;zi=0;
         pocet=0;
         do {
            zr2=zr*zr-zi*zi;
            zi2=2*zr*zi;
            zr=zr2+cr;
            zi=zi2+ci;
            pocet++;
         }
         while ((pocet<limit) && ((zr*zr+zi*zi)<=4));
         if(pocet==limit) g2.setColor(Color.black);
         else g2.setColor(Color.white);
         g2.drawLine(i,j,i,j);
      }
}

A tu je zodpovedajúca procedúra na kreslenie množiny v Delphi Pascale:

procedure TFormMandelbrot.KresliMnozinu;
var limit,pocet,i,j:integer;
    cr,ci,zr,zi,zr2,zi2:real;
begin	
 limit:=256;
 for i:=0 to 400 do
   for j:=0 to 400 do
     begin
       cr:=(i-200)/100; 
       ci:=(200-j)/100;
       zr:=0;
       zi:=0;
       pocet:=0;
       repeat
         zr2:=zr*zr-zi*zi;
         zi2:=2*zi*zr;
         zr:=zr2+cr;
         zi:=zi2+ci;
         pocet:=pocet+1;
       until (pocet>=limit) or ((zr*zr+zi*zi)>4);
       if pocet=limit then image.canvas.pixels[i,j]:=clBlack
       else image.canvas.pixels[i,j]:=clWhite;
     end;
end;

Najlepšie by bolo, keby ste si teraz sami skúsili napísať svoj vlastný program, ktorý vykreslí Mandelbrotovu množinu! Tým, že to urobíte, si najlepšie preveríte to, či ste pochopili výklad na týchto stránkach. A nič nechutí viac ako pocit uspokojenia z vlastného úspechu!