Späť Virtuálne laboratórium Ďalej

F. Mandelbrotova množina

OBSAH:

Úvod

A.
Mandelbrotova množina z nadhľadu

B.
Čo sú to komplexné čísla?

C.
Operácie s komplexnými číslami

D.
Skúsme si to!

E.
Jedna obyčajná funkcia

F.
Mandelbrotova množina

G.
Algoritmus

H.
Odkazy
Na jeho veľké prekvapenie bola rastúca chaotičnosť znakom niečoho skutočného. Z hlavného ostrova sa lenivo odvíjali výhonky a úponky. Mandelbrot pozoroval ako sa zdanlivo hladké rozhranie štiepi do reťazca špirál, podobajúcich sa na chvosty morských koníkov. Iracionálno tu oplodňovalo racionálno.
James Gleick, Chaos


Na tejto stránke sa nachádza Java applet, ktorý vám umožní na vlastnú päsť preskúmať Mandelbrotovu množniu. Prečítaje si pokyny pod appletom.

Pokyny: Počkajte, kým sa nevygeneruje obrázok Mandelbrotovej množiny. Potom stlačenou myšou vyberte oblasť, ktorá sa má zväčšiť. V dolnej časti appletu sa nachádza číselné vymedzenie práve zobrazenej časti Gaussovej roviny. Dve tlačítka so šípkami vám umožnia vrátiť sa späť k predchádzajúcim výberom, prípadne potom, čo sa vrátite späť, umožnia vám vrátiť sa aj k výberom, z ktorých ste sa vrátili. Ich funkčnosť je podobná ako funkčnosť podobných tlačítok v internetových prezeračoch. Ak myšou do obrázku iba kliknete, applet sa vráti k pôvodnej, celej množine. Pre lepšiu orientáciu je v ľavom dolnom rohu po vybratí nového výberu zobrazený predchádzajúci výber a v ňom je bielym štvorčekom znázornený nový výber.

Farby: Každému bodu obrázku je priradená spektrálna farba, ktorá súvisí s počtom opakovaní pocet rekurentného výpočtu členov pomocnej postupnosti, prislúchajúcej tomuto bodu, ktorý je potrebné vykonať, aby orbita pomocnej postupnosti prekročila hraničnú kružnicu. Farbenie bodov je zrejmé z nasledujúceho obrázka:

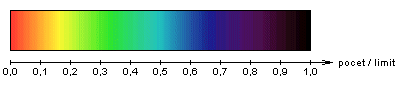
Spektrum

Body, ktoré v danom priblížení považujeme (pre danú, zvolenú hodnotu limit) za body Mandelbrotovej množiny, sú čierne.

To, ako sa Mandelbrotova množina v applete zobrazí, závisí na hodnote premennej limit, ktorá predstavuje maximálny počet členov postupnosti, ktorý applet vypočíta, aby rozhodol, či daný bod patrí, alebo nepatrí do Mandelbrotovej množiny. Je zaujímavé, skúsiť hodnotu limit zmeniť a pozrieť sa na to, aký má jej veľkosť vplyv na obrázok množiny v applete.

ÚLOHA F1: Meníme premennú limit

V applete je hodnota premennej limit nastavená na 256. Túto hodnotu však môžete zmeniť. Dole, pod touto úlohou, sa nachádza textové políčko, do ktorého napíšte novú hodnotu premennej limit. Potom kliknite na modrý odkaz nastavLimit(). V applete sa tak nastaví vami zvolená hodnota premennej limit. Preskúmajte, ako sa bude meniť znázornená Mandelbrotova množina, keď budeme hodnotu limit zväčšovať! Bude sa plocha množiny (čierna oblasť) pritom zväčšovať, alebo zmenšovať? Prečo?

nastavLimit()

Benoit Mandelbrot objavil Mandelbrotovu množinu v roku 1979, keď pracoval pre spoločnosť IBM. Dostal sa k nej pri štúdiu iných, tzv. Juliových množín. Viac sa o histórii Mandelbrotovej množiny môžete dozvedieť napríklad v Gleickovej knihe Chaos (viď stránku H. Odkazy.)

Benoit Mandelbrot

Benoit Mandelbrot, *1924

Na nasledujúcej stránke sa pozrieme na algoritmus, podľa ktorého si môžete sami na počítači nakrelsiť svoju vlastnú Mandelbrotovu množinu.
Späť Virtuálne laboratórium Ďalej