
E. Jedna obyčajná funkcia
OBSAH:
ÚvodA.
Mandelbrotova množina z nadhľadu
B.
Čo sú to komplexné čísla?
C.
Operácie s komplexnými číslami
D.
Skúsme si to!
E.
Jedna obyčajná funkcia
F.
Mandelbrotova množina
G.
Algoritmus
H.
Odkazy
Funkcia sa predstavuje
To, čo na Mandelbrotovej množine prekvapuje asi najviac, je protiklad medzi jej zložitosťou a jednoduchosťou funkcie, ktorá ju vytvára. V ďalšom sa pozrieme na funkciu komplexnej premennej, ktorá má na svedomí celú krásu Mandelbrotovej množiny.
Najprv však krátko o tom, čo sú to funkcie komplexnej premennej. Sú to funkcie, ktoré každému komplexnému číslu zo svojho definičného oboru priradia nejaké, vo všeobecnosti iné, komplexné číslo. Alebo ak chcete, funkcia komplexnej premennej sa dá chápať ako automat, do ktorého vhodíte jeden vektor v Gaussovej rovine a on ako reakciu na váš počin, vychrlí iný vektor v Gaussovej rovine.
Nás bude zaujímať funkcia
|
f(z) = z 2 + c, |
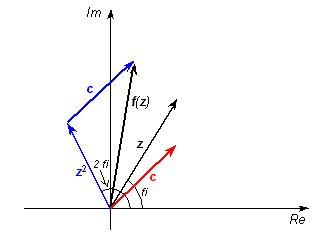
Čo urobí s číslom z táto funkcia? Najprv ho otočí tak, aby zvieralo s osou x dvojnásobný uhol (pri násobení z * z sa uhol prislúchajúci číslu z sčíta sám so sebou), potom ho natiahne alebo stlačí tak, aby malo veľkosť rovnú druhej mocnine predchádzajúcej veľkosti a napokon k nemu pripočíta konštantu c.
Na konkrétnom príklade to vidíte na nasledujúcom obrázku.
|
V znázornenom prípade sa číslo c = 0,3713 + 0,3544*i, číslo z = 0,3835 + 0,6175*i a f(z) = 0,1371 + 0,8280*i. Najprv sa zo z vypočítalo číslo z2 (spodný modrý vektor) a k nemu sa pripočítalo číslo c (horný modrý vektor). V konečnom dôsledku funkcia f priradila číslu z číslo f(z). |
Definičným oborom našej funkcie f je zrejme množina všetkých komplexných čísel, keďže popísaný proces sa dá urobiť s ľubovoľnou šípkou v Gaussovej rovine.
Ako vypočítať funkciu f algebraicky?
Počítač nepozná komplexné čísla. Preto preň musíme funkciu f definovať tak, aby ju bol schopný vypočítať. Využijeme vedomostí, ktoré ste získali na stránke C.
Majme teda komplexné číslo z, dané svojou reálnou a imaginárnou časťou
z = zr + zi *i.
Podobne nech je dané aj číslo c = cr + ci * i.
Podľa vzťhu pre násobenie komplexných čísel z časti C bude
z2 = (zr2 – zi2) + (2*zr*zi) * i .
Ak ku z2 pripočítame číslo c, dostaneme podľa vzťahu pre sčítanie v časti C výsledok
f(z) = (zr2 – zi2 + cr) + (2*zr*zi + ci) * i
Zhrňme to:
|
Ak z = zr + zi *i a c = cr + ci * i, |
Pomocná postupnosť komplexných čísel
Ako môže s takej jednoduchej funkcie vzniknúť niečo také zložité ako Mandelbrotova množina? Tajomstvo spočíva v tom, že pri kreslení Mandelbrotovej množiny počítač počíta túto funkciu mnohokrát za sebou. Hovoríme, že ju iteruje. Čo pod tým konkrétne myslíme?
Keď chce počítač ofarbiť niektorý bod na obrazovke (teda zistiť, či jemu prislúchajúce číslo c z komplexnej roviny leží alebo neleží v Mandelbrotovej množine), musí vygenerovať pomocnú postupnosť komplexných čísel
{z0, z1, z2, z3, ...},
ktorá je daná rekurentne nasledujúcim spôsobom:
z0 = 0
zn+1 = f(zn),
kde f je naša funkcia f(z) = z2 + c.
Čo to znamená? Na začiatku pozná počítač len konštantu c a nultý člen postupnosti, komplexné číslo z0 = 0. Prvý člen postupnosti vypočíta ako z1 = f(z0). Už teda pozná dva členy postupnosti. Ďalší člen vypočíta ako z2 = f(z1), ďalší člen ako z3 = f(z2), atď. Tak môže počítať člen za členom všetky členy postupnosti. Pritom neustále používame funkciu f, pričom jej hodnotu v danom kroku výpočtu berieme ako argument pre ďalší krok. Hovoríme, že funkciu f iterujeme. Členy pomocnej postupnosti nazývame iterácie funkcie f.
Na základe vlastností tejto postupnosti potom počítač v rámci svojich možností rozhodne, akú farbu priradiť bodu na obrazovke, ktorý zodpovedá komplexnému číslu c.
Skúste si to!
Nasledujúci Java applet vám umožní preskúmať rôzne pomocné postupnosti a zistiť od čoho závisia a ako sa správajú. Riešte postupne úlohy nasledujúce za appletom. Pri ich riešení sa zoznámite s niektorými novými pojmami a hlavne sa konečne dozviete, čo je Mandelbrotova množina.
|
|
Pre začiatok si všimnime niektoré vlastnosti appletu.
|
Úloha E1 |
Táto kružnica bude v ďalšom hrať veľmi dôležitú rolu. Nazývame ju hraničná kružnica. Podrobnejšie si o jej polomere pohovoríme ešte neskôr.
Okrem toho je v zobrazovacej ploche znázornené červenou farbou komplexné číslo c. Jeho hodnotu si môžete prečítať v páse napravo od zobrazovacej plochy.
Okrem čísla c je zobrazený aj nultý člen pomocnej postupnosti, z0. Keďže je to nula, prislúcha mu vektor s nulovou dĺžkou.
Na pravej strane appletu sa nachádza ovládací panel. V jeho dolej časti sú tri tlačítka. V hornej časti sú ovládacie bloky ZOBRAZIŤ a ZOOM, s ktorými sa oboznámime neskôr.
|
Úloha E2 |
Rovnako ako predtým, aj teraz applet znázornil grafický súčet vektorov z12 a c. Z appletu je vidieť, že tento súčet sa rovná číslu z2.
|
Úloha E3 |
Všimnite si, že konce členov postupnosti sú spojené červenou lomenou čiarou. Tejto čiare sa hovorí orbita prislúchajúca číslu c. Je jasné, že orbita je daná pomocnou postupnosťou. Ak poznáme pomocnú postupnosť, poznáme aj orbitu, a naopak.
|
Úloha E4 |
|
Úloha E5 |
Áno! Presne tak! Pochopili ste správne:
|
Ak orbita pomocnej postupnosti prekročí hraničnú kružnicu, číslo c, ktorým je postupnosť daná, nepatrí do Mandelbrotovej množiny. |
Toto platí dokonca ako ekvivalencia, ktorú možno chápať ako definíciu Mandelbrotovej množiny:
|
Číslo c, ktorým je pomocná postupnosť daná, nepatrí do Mandelbrotovej množiny práve vtedy keď orbita postupnosti prekročí hraničnú kružnicu. |
Alebo ešte inak:
|
Číslo c, ktorým je pomocná postupnosť daná, patrí do Mandelbrotovej množiny práve vtedy keď orbita postupnosti nikdy neprekročí hraničnú kružnicu. |
|
Úloha E6 |
|
Úloha E7 |
Máme istotu, že postupnosť nikdy neprekročí hraničnú kružnicu? Nie! Túto istotu nemá ani applet, preto vypísal, že číslo c pravdepodobne patrí do Mandelbrotovej množiny. Pravdepodobne. Ale nie určite. Môže sa napríklad stať, že pri 1252. člene by postupnosť hraničnú kružnicu prekročila. Lenže my (a ani applet) nemáme nekonečnú trpezlivosť ani neobmedzené zásoby času, aby sme overili všetky členy postupnosti. Nestačil by nám na to ani vek Vesmíru. Robíme aspoň čo môžeme ...
Overiť, že dané číslo c patrí do Mandelbrotovej množiny teda nie je možné. Uchyľujeme sa preto ku kompromisu. Zvolíme maximálny počet členov postupnosti, ktoré budeme preverovať (označme ho limit) a ak orbita postupnosti po preverení tohto počtu členov neprekročí hraničnú kružnicu, prehlásime (no nie so stopercentnou istotou), že číslo c patrí do Mandelbrotovej množiny.
V tomto zmysle číslo c = – 0,5100 + 0,5800 * i v applete patrí do Mandelbrotovej množiny. Hodnota maximálneho počtu členov postupnosti má v applete pevne nastavenú hodnotu limit = 256.
Objavuje sa Mandelbrotova množina!
Teraz by ste v tom zmysle, ako sme to pred chvíľkou vysvetlili, vedeli o každom bode Gaussovej roviny rozhodnúť, či patrí alebo nepatrí do Mandelbrotovej množiny. V princípe by bolo možné vybrať si dve farby, povedzme bielu a sivú a každý bod Gaussovej roviny zafarbiť na bielo, ak jemu prislúchajúce číslo c nepatrí do Mandelbrotovej množiny a na sivo, ak do nej patrí.
Bola by to však príšerne zdĺhavá a pre človeka vyčerpávajúca práca. Na takýto druh úloh máme počítače. Necháme preto applet, aby sám, bod po bode, prešiel cez všetky body obrazovky a zodpovedajúco ich zafarbil.
|
Úloha E8 |
Limitné cykly
Teraz sa podrobnejšie pozrieme na správanie sa orbít, ktoré prislúchajú bodom c zvnútra Mandelbrotovej množiny. Budeme si všímať, ako sa správajú. Na to, aby sme mohli ich správanie pozorovať, bol applet uspôsobený tak, že vždy zobrazuje len posledných 32 členov pomocnej postupnosti (a teda posledných 32 úsekov orbity). To nám umožní skúmať správanie orbity vtedy, keď je už vypočítaných dostatočne veľa členov postupnosti.
|
Úloha E9 |
Ak ste postupovali podľa návodu, mali by ste dospieť k záveru, že orbita sa po špirále postupne zbieha do nejakého bodu. Tomuto bodu sa hovorí pevný bod alebo tiež limitný cyklus s periódou 1. Keďže tento bod orbitu akoby priťahuje, predstavuje špeciálny prípad atraktora (v angličtine to attract = priťahovať). Orbita je k nemu priťahovaná a od istého člena sa už jej členy prakticky zhodujú s atraktorom a už sa nemenia. S inými typmi atraktorov sa oboznámime o chvíľu.
|
Úloha E10 |
Mali by ste pozorovať, že po istom čase bude orbita oscilovať medzi dvoma bodmi v Gaussovej rovine. Orbita sa znovu pritiahla k atraktoru, tentoraz iného typu. Hovoríme, že sa usadila na limitnom cykle s periódou 2.
|
Úloha E11 |
Mali by ste pozorovať, že po istom čase bude orbita oscilovať medzi tromi bodmi v Gaussovej rovine. Hovoríme, že orbita sa usadila na limitnom cykle s periódou 3.
|
Úloha E12 |
Mali by ste pozorovať, že orbita sa neusadí na žiadnom limitnom cykle. Nemá periodický charakter. Hovoríme, že sa usadila na chaotickom atraktore.
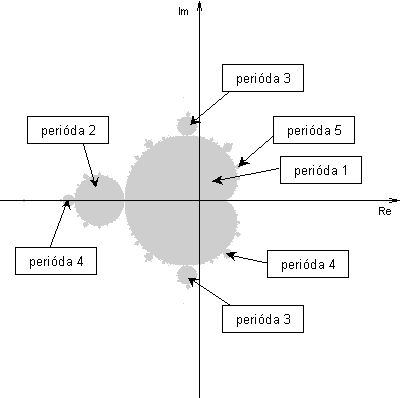
Ako vidíte, svet Mandelbrotovej množiny skrýva množstvo tajomstiev. Z hlavnej kardiotidy Mandelbrotovej množiny vyrastá mnoho kruhových výhonkov. Z nich vyrastajú ďalšie, menšie kruhové výhonky. Mohlo by byť zábavné preskúmať periódu limitného cyklu na ktorom sa usadí orbita, v závislosti na vybratom kruhovom výhonku.
|
Úloha E13 (posledná) |
Pre priateľov matematiky
Pre úplnosť a poriadok uvedieme teraz pre priateľov matematiky (a teda aj presnosti) niekoľko spresnení. Výklad bude strohejší, ale aj presnejší. Tí z vás, pre ktorých nie je matematika srdcovou záležitosťou, môžete zvyšok tejto stránky preskočiť. Nebude vám v ďalšom výklade chýbať, až na to, že neuvidíte niektoré súvislosti.
Najprv musíme spresniť definíciu Mandelbrotovej množiny. Tu je:
|
Definícia: (Mandelbrotova množina) |
Z definície vyplýva, že bod c nepatrí do Mandelbrotovej množiny vtedy, keď jemu prislúchajúca pomocná postupnosť rastie nad všetky medze. Predtým, v texte stránky, sme tvrdili, že na to, aby bod c nepatril do množiny, stačí ak pomocná postupnosť prekročí hraničnú kružnicu s polomerom 2. V ďalšom ukážeme, že ak sa to stane, tak pomocná postupnosť už bude určite rásť nad všetky medze a jej orbita skončí v nekonečne. Tým dáme do súladu obe definície, tú z textu, aj tú presnejšiu.
Vetu, ktorej obsahom je toto tvrdenie, sme nazvali Veta o veľkosti hraničnej kružnice. Budú jej predchádzať dve jednoduché lemy (pomocné vety). Dôkaz samotnej vety nie je príliš náročný a mali by ho zvládnuť gymnazisti po skončení tretieho ročníka.
|
Lema 1 (Trojuholníková nerovnosť) |
|
Dôkaz: 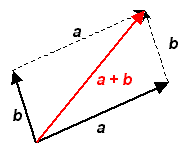 Rovnosť nastane v prípade, že sú vektory a, b súhlasne alebo nesúhlasne rovnobežné. Tvrdenie vtedy zrejme platí. q.e.d. |
|
Lema 2 (Modifikovaná trojuholníková nerovnosť) |
|
Dôkaz: |
|
Veta o veľkosti hraničnej kružnice |
|
Dôkaz: a.) Prípad |c| ≤ 2 Nech zk je prvý taký člen postupnosti, ktorý spĺňa nerovnosť |zk| >2. Pozrieme sa, čo platí pre veľkosť nasledujúceho člena postupnosti zk+1 :
Použili sme pritom modifikovanú trojuholníkovú nerovnosť (lemu 2). Teraz využijeme, predpoklad vety a to, že |c| ≤ 2: |zk| > 2 ≥ |c| Vynásobíme poslednú nerovnosť číslom (–1) a dostaneme: –|zk| < –2 ≤ –|c| Z toho vyplýva, že –|c| > –|zk| . Ak teraz k poslednej nerovnosti pripočítame číslo |zk|2, dostaneme
Ak spojíme nerovnosť (1) a (2) dostaneme: |zk+1| > |zk|2 – |zk| = (|zk| – 1) |zk| Teda
Keďže |zk| > 2, bude |zk| – 1 > 1. Teda činiteľ v zátvorke vo vzťahu (3) je väčší ako 1. Ak ním vynásobíme číslo |zk|, ktoré je väčšie ako 2, bude súčin zaručene väčší ako 2. Preto bude zrejme číslo zk+1 spĺňať vzťah |zk+1| > |zk| > 2. Teraz by sme mohli rovnakú argumentáciu ako pre číslo zk použiť aj pre číslo zk+1, lebo preň platí |zk + 1| > 2. Dostali by sme, že
Ak uvážime nerovnosť (3), dostaneme
Tento postup možno zopakovať ľubovoľne veľa krát. Pre veľkosť člena postupnosti zk+n môžeme takto napísať dve zovšeobecnenia:
Z nich vyplýva, že všetky členy postupnosti nasledujúce za k–tym členom už majú veľkosť väčšiu ako 2. Ďalej súčiniteľ v zátvorke vzťahu (6) je väčší ako 1. To znamená, že postupnosť veľkostí je rastúca, t.j. |zk| < |zk+1| < |zk+2| < |zk+3| < |zk+4| . . . Ako však ukázať, že veľkosti členov postupnosti rastú nad všetky medze? Na to použijeme malý trik. Budeme potrebovať nejakú pomocnú postupnosť {d0, d1, d2, d3, ...} reálnych čísel, o ktorej budeme s istotou vedieť, že rastie nad všetky medze. Ukážeme, že každý člen postupnosti {|zk|, |zk+1|, |zk+2|, |zk+3|, ...} je vždy väčší ako jemu zodpovedajúci člen pomocnej postupnosti, t.j. ukážeme, že pre každé n platí dn < |zk+n | To bude znamenať, že ak nad všetky medze rastie pomocná postupnosť, tak musí nad všetky medze rásť aj postupnosť, ktorú vyšetrujeme. Stačí už len nájsť takú pomocnú postupnosť a ukázať, že má vyhovujúce vlastnosti. Označme teda symbolom q reálne číslo q = |zk| – 1. Budeme uvažovať pomocnú geometrickú postupnosť dn = qn |zk|. Pritom q je jej kvocient. Keďže q > 1, táto geometrická postupnosť rastie nad všetky medze. Vráťme sa ku vzťahu (7): |zk+n| > (|zk+n–1| – 1) (|zk+n–2| – 1). . . (|zk+1| – 1) (|zk| – 1) |zk| (7) opakovaný
Keďže |zk+1| > |zk|, bude zrejme platiť aj |zk+1| – 1 > |zk| – 1 = q, teda |zk+1| – 1 > q Podobne sa dá ukázať, že Všetky súčinitele v zátvorkách vzťahu (7) okrem |zk| – 1 sú väčšie ako q. Preto |zk+n | > qn |zk| Podarilo sa nám teda dokázať, že pre každé n platí dn < |zk+n|. To znamená, že postupnosť komplexných čísel {z0, z1, z2, z3, ...} spĺňajúca predpoklady vety, rastie v prípade, že |c| ≤ 2, nad všetky medze. b.) Prípad |c| > 2 Nie je ťažké vidieť, že v tomto prípade je prvým členom postupnosti, ktorý má väčšiu veľkosť ako 2, už člen z1 = c. Pre nasledujúci člen bude platiť: |z2| = |z12 + c| = |c2 + c| ≥ |c|2 – |c| = (|c| –1)|c| Využili sme pritom znovu modifikovanú trojuholníkovú nerovnosť (lema 2). Posledná zátvorka je väčšia ako 1 (lebo |c| > 2), takže bude zrejme platiť, že |z2| > |c| > 2 Pre nasledujúci člen budeme môcť zapísať: |z3| = |z22 + c| ≥ |z2|2 – |c| > |z2|2 – |z2| = (|z2| – 1)|z2| Okrem lemy 2 sme teraz využili aj fakt, že |z2| > |c| a teda –|c| > –|z2|. Člen v zátvorke je znovu väčší ako 1, takže aj pre z3 bude platiť: |z3| > |z2| > |c| > 2 Navyše |z3| > (|z2| – 1)(|c| –1)|c| Takto by sa dalo pokračovať do nekonečna. Tým by sme dokázali, že pre n–tý člen postupnosti platí: |zn| > |zn–1| > . . . > |z3| > |z2| > |c| > 2 |zn| > (|zn–1| – 1) . . . (|z2| – 1) (|c| – 1) |c| Z toho vyplýva, že postupnosť veľkostí členov vyšetrovanej postupnosti je rastúca. To, že rastie nad všetky medze sa dokáže podobne, ako v časti a.) dôkazu. Stačí porovnať túto postupnosť s geometrickou postupnosťou s kvocientom väčším ako 1, ktorá zaručene diverguje. Nechceme sa opakovať a preto dokončenie dôkazu prenecháme na čitateľa. q.e.d. |