A. Mandelbrotova množina z nadhľadu

OBSAH:

Obdivovatelia Mandelbrotovej množiny často hovoria, že je to najzložitejší matematický objekt. Ani za nekonečne dlhý čas by sme si ju nestačili celú prezrieť. Kotúče ozdobené ostrými tŕňmi, rozvíjajúce a vinúce sa špirály a vlákna, na ktorých visia rozmanité cibuľovité molekuly, sa podobajú na bobule hrozna zo súkromnej vinice Boha. Ak pozorujeme Mandelbrotovu množinu nastaviteľným oknom počítačovej obrazovky vo farbách, zdá sa nám byť ešte fraktálovitejšia ako samotné fraktály, natoľko je jej zložitosť v rôznych mierkach bohatá. Súpis rôznych obrázkov, ktoré ju tvoria, alebo numerický opis obrysov množiny by vyžadovali nekonečné množstvo informácií. Ale je tu jeden paradox: na prenos úplného popisu množiny elektrickým vedením stačí len zopár desiatok znakov kódu. Stručný počítačový program obsahuje dostatok informácií na reprodukciu celej množiny. Tí, ktorí prví pochopili, ako sa v tejto množine spája zložitosť s jednoduchosťou, neboli na to pripravení, dokonca ani sám Mandelbrot. Mandelbrotova množina sa stala verejným symbolom teórie chaosu, ktorý sa objavoval na titulných stranách zborníkov z konferencií a na odborných časopisoch. Bola jadrom výstavy počítačového umenia, ktorá v rokoch 1985 a 1986 cestovala po svete. Z obrázkov bola jej krása ľahko uchopiteľná; ťažšie sa jej význam chápal matematikom, ktorí sa jej pomaly učili porozumieť.

James Gleick, Chaos

Ako sa hovorí, lepšie raz vidieť ako stokrát počuť. Pravdivosť Gleickových slov pochopíte až vtedy, keď sa na Mandelbrotovu množinu pozriete sami. Na nasledujúcej sérii obrázkov vám ponúkame záznam cesty do hlbín Mandelbrotovej množiny. Každý nasledujúci obrázok obsahuje detailné zobrazenie výrezu z predchádzajúceho obrázku.

Všimnite si, že Mandelbrotova množina je približne sebepodobný útvar. To znamená, že obsahuje časti, ktoré sa približne podobajú na celú množinu.

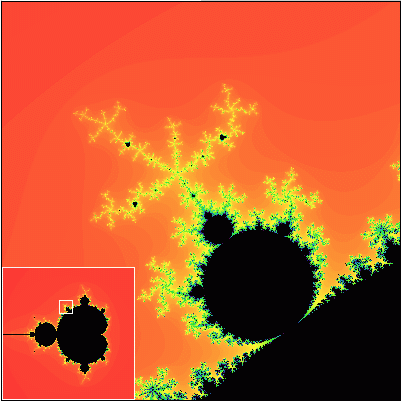
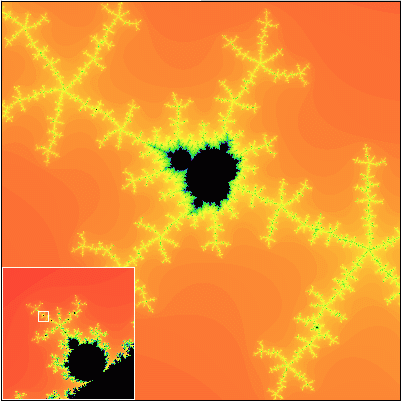
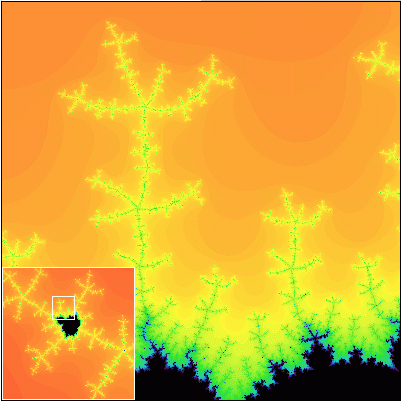
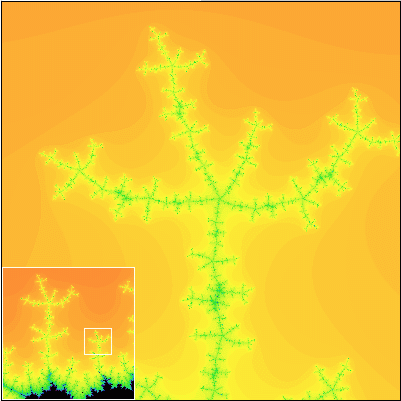
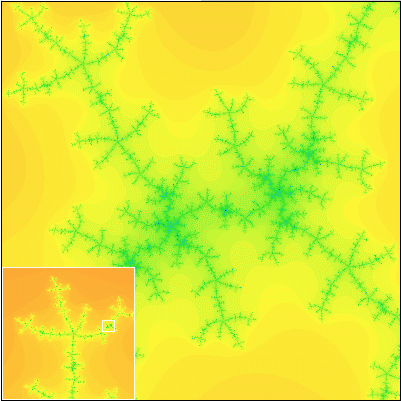
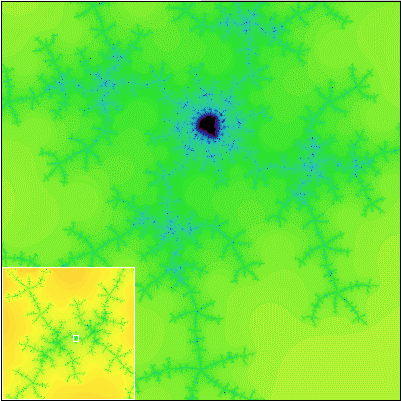
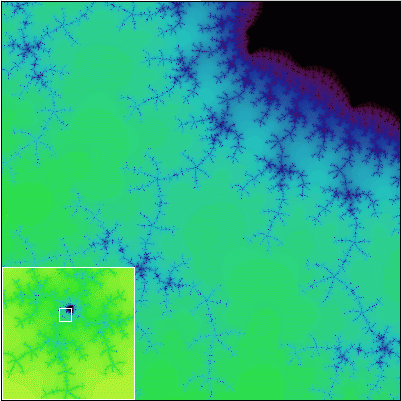
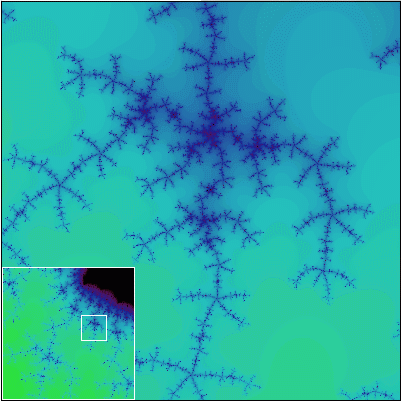
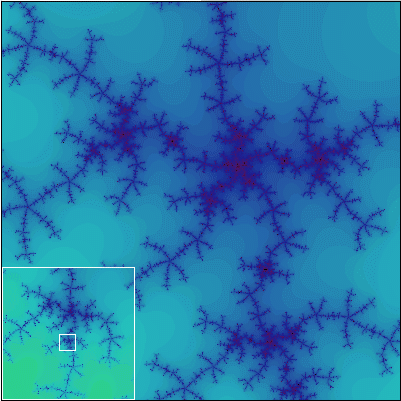
Tak čo? Nadchla vás krása Mandelbrotovej množiny? Ak áno, ste pripravení na to, aby ste preskúmali túto množinu podrobnejšie. Na ďalších stránkach sa dozviete, čo presne Mandelbrotova množina je a tiež to, ako ju možno nakresliť na počítači.

Musíme vás však už tu upozorniť, že pri hlbšom pochopení Mandelbrotovej množiny sa nezaobídeme bez matematiky. Ak ste totálnym nepriateľom matematiky a nezaujíma vás definícia množiny, ani spôsob, ako ju nakresliť, môžete nasledujúce stránky preskočiť a pozrieť sa rovno na Java applet na stránke F, pomocou ktorého budete môcť skúmať Mandelbrotovu množinu na vlastnú päsť.