C. Operácie s komplexnými číslami

OBSAH:

S komplexnými číslami môžeme vykonávať také isté operácie ako s reálnymi číslami, napríklad môžeme ich sčítavať, odčítavať, násobiť, deliť, umocňovať alebo odmocňovať. Všetky tieto operácie sú analogické operáciám s reálnymi číslami. Najprv si tu uvedieme ich stručný prehľad a potom si na nasledujúcej stránke precvičíte prebrané operácie na jednoduchom Java applete.

Hlavne sa nevydeste z matematiky na tejto stránke! Chvíľku to vydržte a potom uvidíte, aké to všetko je jednoduché!

Sčítavanie komplexných čísel

Dve komplexné čísla sčítavame tak, že sčítavame ich vektory. Do koncového bodu vektora prvého čísla umiestnime začiatočný bod vektora druhého čísla. Výsledkom je vektor, ktorý spája začiatočný bod vektora prvého čísla s koncovým bodom vektora druhého čísla. Výsledkom sú koncové súradnice výsledného vektora v Gaussovej rovine.

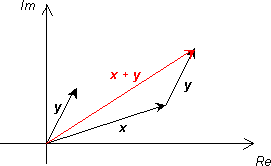
Sčítanie dvoch komplexných čísel.

Súčet dvoch komplexných čísel možno urobiť aj algebraicky: Majme dve komplexné čísla, (a + b*i) a (c + d*i). Ich súčet vypočítame ako (a + b*i) + (c + d*i) = a + c + b*i + d*i = [(a +c) + i*(b + d)]. Vidíme, že súčtom dvoch komplexných čísel je znovu komplexné číslo, ktorého reálna časť je (a + c) a imaginárna časť je (b + d).

Ak chceme sčítať viac komplexných čísel, najprv sčítame podľa vyššie uvedeného spôsobu dve čísla, potom k výslednému vektoru pripočítame vektor tretieho čísla atď.

Odčítavanie komplexných čísel

Postupujeme tým istým spôsobom ako pri sčítavaní. Do koncového bodu vektora prvého čísla umiestnime začiatočný bod vektora druhého čísla, ale tento vektor bude otočený o 180° oproti pôvodnému vektoru druhého čísla. Výsledným vektorom je opäť spojnica začiatočného bodu vektora prvého čísla a koncového bodu vektora druhého čísla.

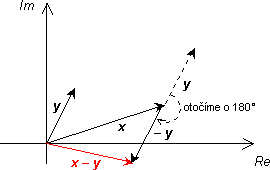
Odčítavanie dvoch komplexných čísel.

Rozdiel dvoch komplexných čísel možno urobiť aj algebraicky: Majme dve komplexné čísla, (a + b*i) a (c + d*i). Ich rozdiel vypočítame ako (a + b*i) – (c + d*i) = a – c + b*i – d*i = [(a – c) + i*(b – d)]. Vidíme, že súčtom dvoch komplexných čísel je znovu komplexné číslo, ktorého reálna časť je (a – c) a imaginárna časť je (b – d).

Pri odčítavaní viacerých komplexných čísel odčítame najprv od vektora prvého čísla vektor druhého čísla, od výsledného vektora vektor tretieho čísla atď.

Násobenie komplexných čísel

Násobenie komplexných čísel definujeme na prvý pohľad trochu čudne. Zahŕňa v sebe dve geometrické transformácie, rovnoľahlosť (t.j. natiahnutie alebo skrátenie) a otáčanie.

Keď v Gaussovej rovine násobíme dvomi reálne číslo 3, dostaneme reálne číslo 6. Jeho vektor je v Gaussovej rovine dvojnásobne natiahnutý oproti vektoru pôvodného čísla 3. Čiže násobenie reálnych čísel môžeme geometricky chápať ako naťahovanie (prípadne skracovanie) vektora pôvodného čísla.

Pri násobení komplexných čísel nevystačíme len s jednou geometrickou transformáciou v rovine. Na pomoc si vezmeme ešte otáčanie. Ak chceme vynásobiť dve komplexné čísla, musíme najprv otočiť proti smeru pohybu hodinových ručičiek prvé číslo o uhol, ktorý zviera druhé číslo s reálnou osou a potom ho ešte musíme natiahnuť na ťoľkonásobok jeho dĺžky, aká je absolútna hodnota druhého čísla. Inak povedané:

Pri násobení dvoch komplexných čísel musíme vypočítať súčet uhlov, ktoré zvierajú vektory daných komplexných čísel s reálnou osou x. Výsledný vektor bude s osou x zvierať uhol rovný súčtu pôvodných uhlov vektorov daných čísel. Veľkosť výsledného vektora bude predstavovať súčin absolútnych hodnôt veľkostí vektorov daných čísel.

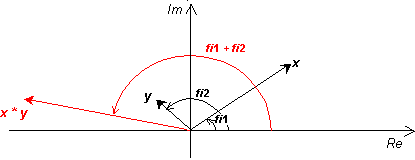
Násobenie dvoch komplexných čísel.

Násobiť viac komplexných čísla znamená vynásobiť najprv dve a potom výsledný vektor vynásobiť tretím komplexným číslom atď.

Podobne ako súčet a rozdiel, nemusíme súčin dvoch komplexných čísel robiť iba graficky. Môžeme ho vyjadriť aj výpočtom. Nech sú dané dve komplexné čísla vo všeobecnom tvare:

Súčin týchto dvoch čísel je:

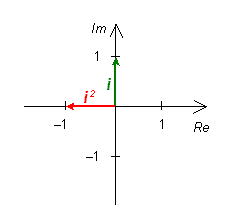
V poslednom zápise sa vyskytuje číslo i umocnené na druhú. Čomu sa rovná tento výraz? Skúsme už s našimi vedomosťami vynásobiť číslo i samo sebou. Vieme, že toto číslo je jednotkový vektor na imaginárnej osi y, čiže zviera s osou x uhol veľkosti 90°. Keď násobíme dané číslo samo sebou, potom súčet uhlov musí byť dvakrát väčší ako pôvodný uhol. Čiže výsledný vektor bude ležať v smere 180° od osi x. Z toho vyplýva, že výsledný vektor bude ležať na osi x, ale v jej zápornej časti. Veľkosť tohoto vektora bude 1*1 = 1, pretože vektor i má veľkosť 1 (jednotkový vektor). Tým zisťujeme, že vektor čísla i² bude ležať na reálnej osi x, bude mať veľkosť 1 a bude orientovaný v jej zápornom smere. Výsledné číslo tým bude mať súradnice [–1;0]. Čiže môžeme napísať slávny vzťah:

Nie je to elegantné odvodenie?

Po vyjadrení i ² = –1 dostávame pre súčin dvoch komplexných čísel vzťah:

V tejto poslednej rovnici je výraz (a*c – b*d) reálnou časťou komplexného čísla (súradnica na osi x) a výraz i*(a*d + b*c) je imaginárnou časťou komplexného čísla (výraz v zátvorke určuje súradnicu a písmeno i pred zátvorkou naznačuje, že ide o súradnicu osi y). Perfektné je to, že sme zistili, že súčinom dvoch komplexných čísel je znovu komplexné číslo! Naša definícia násobenia je teda v poriadku.

Delenie komplexných čísel

Budeme struční, keďže delenie nebudeme priamo v pochopení Mandelbrotovej množiny potrebovať.. Postupujeme podobne ako pri násobení, ale uhly, ktoré zvierajú vektory daných čísel s reálnou osou x nesčítavame, ale odčítavame. Taktiež veľkosť výsledného vektora bude daná podielom veľkostí vektorov daných čísel.

Algebraický výpočet podielu dvoch komplexných čísel tu neuvádzame, keďže ho nebudeme nikde potrebovať.

Na nasledujúcej stránke si priamo na Java applete vyskúšate ako funguje sčítanie, odčítanie, násobenie a delenie komplexných čísel. Potom už budete dostatočne pripravení na to, aby ste si mohli trúfnuť na podrobnejší pohľad na samotnú Mandelbrotovu množinu.