B. Čo sú to komplexné čísla?

OBSAH:

Predtým ako sa aj my spolu s pánom Mandelbrotom ponoríme do podrobnejšieho štúdia úžasného sveta Mandelbrotovej množiny si budeme musieť trochu precvičiť svoje mozgové závity. Dôvod je jednoduchý. Mandelbrotova množina je "napísaná" v jazyku matematiky, presnejšie v jazyku komplexných čísel. Bez nich by sme sa v porozumení Mandelbrotovej množine nezaobišli. Poďme teda na to!

Väčšina ľudí pozná iba reálne čísla (8; 2,4; 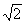; atď.). Nachádzajú sa v jednom rade pekne usporiadané podľa veľkosti. Tento rad reálnych čísel nazývame číselná os. Číselná os má rozmedzie od mínus nekonečna – 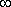až po plus nekonečno + 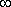. Keď si túto os predstavíme ako priamku, ktorá leží v rovine, logicky sa spýtame, či aj v iných bodoch roviny okrem bodov tejto priamky môžeme nájsť nejaké čísla.

Nemecký matematik Carl Friedrich Gauss (1777 - 1855)

Ukazuje sa, že áno. Aj v iných miestach roviny sa nachádzajú čísla. Tieto čísla nazývame imaginárne čísla. Dokopy so všetkými reálnymi číslami tvoria množinu všetkých komplexných čísel. Definoval ich nemecký matematik Gauss a podľa neho sa aj táto rovina čísel pomenovala Gaussova rovina. Túto rovinu rozdeľujú dve osi — už spomínaná číselná os, ktorú budeme pokladať za os x (reálna os) a na ňu kolmá os y (imaginárna os). Obe tieto osi sa pretínajú v bode [0;0].

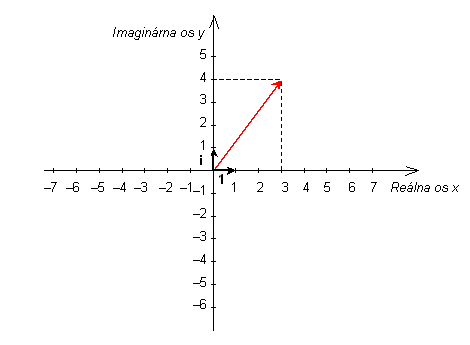
Komlexné číslo 3 + 4*i v Gaussovej rovine.

Komplexné čísla sa od reálnych líšia svojím zápisom. Kým na zápis reálneho čísla potrebujeme iba jedno reálne číslo, ktoré určuje jeho polohu na číselnej osi, na zápis komplexného čísla potrebujeme dve reálne čísla. Jedno určuje, reálnu časť komplexného čísla — jeho priemet do osi x — a druhé jeho imaginárnu časť — jeho priemet do osi y. Komplexné číslo potom zapíšeme ako výraz a + b*i, kde a je jeho reálna časť, b je jeho imaginárna časť a i je jednotkový vektor v Gaussovej rovine v smere imaginárnej osi y. Podobne je číslo 1 jednotkovým vektorom v smere osi x. Na osi x je napríklad číslo 8 dané ako 8-násobok jednotkového vektora 1, t.j. 8 = 8*1. Tento jednotkový vektor však kvôli úspornosti nepíšeme. V druhom člene výrazu však musíme použiť písmeno i, keďže neide o reálne číslo. Čiže zápis čísla uvedeného na obrázku bude takýto: 3 + 4*i.

Zápisu komplexných čísle v tvare a + b*i, kde a, b sú reálne čísla hovoríme algebraický tvar komplexných čísel. Z obrázku vidíme, že každé komplexné číslo v rovine môžeme zaznačiť ako vektor so začiatkom v bode so súradnicami [0;0] a koncom v súradniciach daných zápisom tohoto čísla, v našom prípade [3;4].

Dve komplexné čísla sú rovnaké práve vtedy, ak vektory, ktoré ich predstavujú sú rovnaké. Pojem väčšie alebo menšie pri komplexných číslach nedefinujeme.

Jestvujú aj ďalšie spôsoby, ktorými môžeme zapísať komplexné číslo. Jedným z nich je goniometrický tvar komplexného čísla. Pri tomto zápise je potrebné poznať dve veci: (1) veľkosť komplexného čísla, t.j. dĺžku šípky, ktorou je znázornené v Gaussovej rovine a (2) uhol ktorý zviera s reálnou osou x. Potom má komplexné číslo tvar

kde c je veľkosť komplexného čísla a fi je uhol, ktorý zviera s reálnou osou. Tento tvar je veľmi jednoducho možné odvodiť z pravouhlého trojuholníka, ktorý vznikne priemetmi vektora komplexného čísla na reálnu a imaginárnu os a zo znalostí funkcií sínus a kosínus. Skúste si to! Je to naozaj jednoduché.

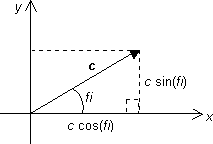
Goniometrický tvar komplexného čísla.

Na ďalšej stránke si povieme niečo o operáciách s komplexnými číslami, ktoré si neskôr ozrejmíme na konkrétnych príkladoch s použítím Java appletu.