A. Môže v polovici nádoby samo od seba vzniknúť vákuum?
OBSAH:
ÚvodA.
Môže v polovici nádoby samo od seba vzniknúť vákuum?
B.
Ekvipartičný teorém
C.
Stavová rovnica
D.
Stredná voľná dráha molekuly
E.
Odkazy
STRUČNÝ OBSAH ČASTI A: |
Makroskopické a mikroskopické sústavy
Vedecký pokrok vo fyzike v minulom storočí nám umožnil nahliadnuť za oponu základných zákonov prírody, popisujúcich správanie sa atómov, molekúl, elektrónov a ďalších, dokonca subjadrových častíc. Vieme napríklad predpovedať, čo sa stane so sústavou dvoch, alebo troch atómov, keď sa nachádza v nejakých, presne daných, začiatočných podmienkach. Dobre rozumieme elektromagnetickým silám, ktoré medzi takýmito atómami pôsobia, poznáme základné zákony kvantovej mechaniky.
To nás môže viesť k záveru, že naša znalosť zákonov fyziky na mikroskopickej úrovni by mala postačovať na to, aby sme mohli v princípe predpovedať vlastnosti ľubovoľnej makroskopickej sústavy častíc, za predpokladu, že poznáme všetky atómy, z ktorých je zložená.
Takýto záver je však prehnane optimistický. Predstavme si, že máme nejaký pohár s vodou, ktorá obsahuje zhruba 1025 navzájom interagujúcich molekúl vody. Predstavme si ďalej, že poznáme na začiatku presný mikroskopický stav takejto sústavy a zadáme ho supervýkonnému počítaču. Počítač naprogramujeme tak, aby na základe známych mikroskopických zákonov pre správanie sa častíc, simuloval časový vývoj molekúl. To by nám umožnilo zistiť, aký je mikroskopický stav molekúl vody v pohári, napríklad po uplynutí jednej hodiny. Vedeli by sme z týchto údajov, ktoré by pozostávali z obrovského počtu (zhruba 1025) čísel, povedať o vode niečo rozumné? Je zmrznutá? Vrie? Je v plynnom, či v kvapalnom skupenstve? Akú má teplotu?
Odpoveď je taká, že by to bolo veľmi komplikované. Superpočítač by nám umožňoval kvantitatívny popis molekúl vody, ale pre nás by bol vhodnejší kvalitatívny popis. (Nezaujímajú nás rýchlosti molekúl, ale napríklad hustota vody.)
Vo fyzike musela vzniknúť nová disciplína, ktorá na takýto druh otázok bola schopná dať uspokojivú odpoveď. Nazýva sa štatistická fyzika. V ďalšom si na jednoduchom príklade plynu pozostávajúceho z niekoľkých molekúl, ukážeme základné metódy skúmania, ktoré štatistická fyzika používa.
Fluktuácie
Jednoduchým príkladom sústavy veľa častíc je plyn pozostávajúci napríklad z atómov hélia. Keď je plyn dostatočne riedky (t.j. počet molekúl pripadajúcich na jednotkový objem je malý), je priemerná vzdialenosť medzi molekulami veľká a preto je ich vzájomné pôsobenie veľmi malé. Plyn nazývame ideálny, ak je taký riedky, že vzájomné pôsobenie medzi jeho jednotlivými časticami je skoro zanedbateľné.
Ideálny plyn je výnimočne jednoduchý. Každá z jeho molekúl strávi väčšinu času pohybom po priamke, konštantnou rýchlosťou, neovplyvnená prítomnosťou iných častíc, alebo stien nádoby. Iba z času na čas sa priblíži k niektorej inej molekule, alebo stene nádoby natoľko, že dôjde k zrážke. Pri zrážkach s inými časticami mení častica zvyčajne smer a veľkosť svojej rýchlosti a teda aj svoju kinetickú energiu.
Uvažujme teraz ideálny plyn pozostávajúci z N molekúl, uzavretých v nádobe tvaru kocky. Budeme predpokladať, že celý systém je izolovaný (t.j. že neinteraguje so žiadnym iným systémom) a že bol ponechaný sám na seba po dostatočne dlhú dobu.
Predstavme si teraz, že by sme takýto film mohli pozorovať prostredníctvom fiktívnej filmovej kamery, ktorá by zaznamenávala polohy molekúl na políčkach filmu tak, že časový rozdiel medzi zosnímaním susediacich políčok by bol t0.
Film z kamery by sme si mohli následne premietnuť a sledovať pohyby jednotlivých molekúl. Hneď by sme zbadali, že každá z molekúl sa správa podľa dobre známych zákonov fyziky pre pohyb častíc. Napriek tomu, keď by bol počet molekúl v zábere veľký, javil by sa nám ich pohyb veľmi chaotický.
Zamerajme teraz svoju pozornosť na polohy molekúl a na ich rozdelenie v priestore. Predpokladajme, že nádoba je rozdelená myslenou priečkou na dve rovnaké časti (viď obr. dole). Označme počet molekúl v ľavej polovici ako n a počet molekúl v pravej polovici ako n'. Zrejme platí, že
n + n' = N
Keby bol celkový počet molekúl veľký, zvyčajne by sme zistili, že n » n', t.j. že v každej polovici nádoby je zhruba rovnaký počet molekúl. Treba však zdôrazniť slovko zvyčajne. Počet molekúl v oboch poloviciach nemusí byť vôbec rovnaký. Niektoré molekuly z ľavej časti odchádzajú, iné tam prichádzajú. Počet molekúl v ľavej časti neustále fluktuuje.
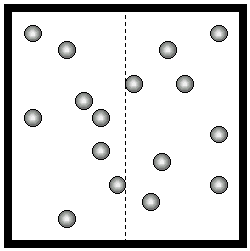
Zvyčajne sú tieto fluktuácie dosť malé, takže n sa len veľmi málo líši od N/2. Neexistuje však nič, čo by zabraňovalo molekulám, aby sa všetky nenahromadili v ľavej časti nádoby (pričom by n = N a n' = 0). Naozaj sa to môže stať. Ale aká je pravdepodobnosť toho, že sa to stane?
Aby sme túto pravdepodobnosť mohli vypočítať, spýtajme sa najprv, koľkými spôsobmi môžeme molekuly rozdeliť do oboch polovíc nádoby. Každý spôsob, akým sa takéto rozdelenie dá urobiť, budeme nazývať konfigurácia. Jednu molekulu môžeme potom v nádobe nájsť v dvoch možných konfiguráciách, lebo môže byť buď v ľavej alebo v pravej polovici. Keďže obe polovice majú rovnaké objemy a sú inak rovnocenné, bude pravdepodobnosť, že molekulu nájdeme vľavo rovnaká ako pravdepodobnosť, že ju nájdeme vpravo.
Uvažujme teraz dve molekuly. Každá z nich môže byť nájdená v ľubovoľnej z oboch polovíc nádoby. Celkový počet konfigurácií (t.j. spôsobov, ktorými dve molekuly možno rozdeliť do dvoch polovíc nádoby) je potom podľa pravidla súčinu 2.2 = 22 = 4, keďže pre každú konfiguráciu prvej molekuly jestvujú dve konfigurácie druhej molekuly (viď obr.)
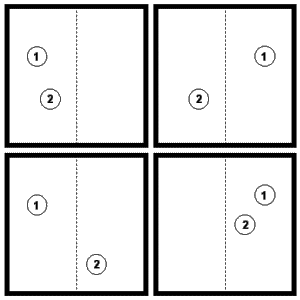
Keby sme uvažovali tri molekuly, bol by celkový počet konfigurácií 2.2.2 = 23 = 8, keďže pre každú z 22 možných konfigurácií prvých dvoch molekúl jestvujú dve konfigurácie tretej. Podobne, ak uvážime všeobecný prípad plynu pozostávajúceho z N molekúl, bude celkový počet možných konfigurácií rovný 2.2.2. ... .2 = 2N. V nasledujúcej tabuľke uvádzame tieto konfigurácie pre špeciálny prípad N = 4 molekuly.
| 1 | 2 | 3 | 4 | n | n' | C(n) |
| Ľ | Ľ | Ľ | Ľ | 4 | 0 |
1
|
|
Ľ Ľ Ľ P |
Ľ Ľ P Ľ |
Ľ P Ľ Ľ |
P Ľ Ľ Ľ |
3 3 3 3 |
1 1 1 1 |
4
|
|
Ľ Ľ Ľ P P P |
Ľ P P Ľ Ľ P |
P Ľ P Ľ P Ľ |
P P Ľ P Ľ Ľ |
2 2 2 2 2 2 |
2 2 2 2 2 2 |
6
|
|
Ľ P P P |
P Ľ P P |
P P Ľ P |
P P P Ľ |
1 1 1 1 |
3 3 3 3 |
4
|
| P | P | P | P | 0 | 4 |
1
|
Molekuly sú označené číslami 1, 2, 3, 4. Písmeno Ľ znamená, že daná molekula sa nachádza v ľavej polovici nádoby, P znamená, že sa nachádza v pravej polovici. Symbolmi n a n' sú označené počty molekúl v ľavej a pravej polovici. C(n) predstavuje počet možných konfigurácií molekúl, keď n z nich sa nachádza v ľavej polovici nádoby.
Všimnime si teraz ako vypočítať vo všeobecnosti C(n). Úloha nájsť C(n), t.j. nájsť počet konfigurácií molekúl, v ktorých sa n z nich nachádza vľavo, je ekvivalentná s kombinatorickou úlohou zistiť, koľkými spôsobmi možno z N molekúl vybrať n molekúl, ktoré potom umiestnime do ľavej polovice nádoby. Pritom nezávisí na poradí, v akom molekuly vyberieme. To čo je dôležité je jedine to, ktoré molekuly vyberieme. Na hodinách matematiky ste takéto úlohy často krát riešili a viete, že počet výberov možno vyjadriť kombinačným číslom
![]()
Počet možných konfigurácií plynu z N
molekúl, v ktorých sa n molekúl nachádza v ľavej časti nádoby je ![]() . Počet všetkých konfigurácií plynu je 2N.
. Počet všetkých konfigurácií plynu je 2N.
Aká je potom pravdepodobnosť P(n), že sa v plyne pozostávajúcom z N molekúl n z nich nachádza v ľavej polovici nádoby? Vyjdeme z predpokladu, že každá konfigurácia je rovnako pravdepodobná. Potom pravdepodobnosť vypočítame ako podiel počtu vyhovujúcich konfigurácií a počtu všetkých konfigurácií.
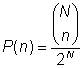
|
Príklad – Plyn zo štyroch molekúl V špeciálnom prípade plynu pozostávajúceho z N = 4 molekúl, budú počty konfigurácií a im zodpovedajúce pravdepodobnosti nasledujúce:
Počty C(n) sú rovnaké ako tie, ktoré sú uvedené v tabuľke prehľadu konfigurácií pre N = 4. |
Na nasledujúcich troch obrázkoch sú znázornené pravdepodobnosti P(n) pre rôzne hodnoty celkového počtu molekúl plynu (N=4, N=10 a N=40). Všimnite si, že vo všetkých prípadoch je pravdepodobnosť maximálna pre n = N/2. Navyše, čím väčšie je N, tým menšia je pravdepodobnosť výskytu situácie s n << N/2, prípadne s n >> N/2.
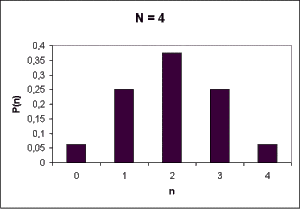
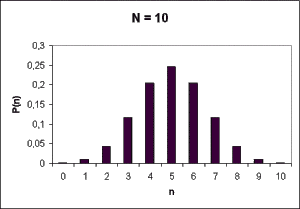
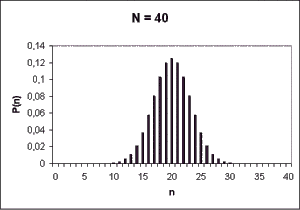
Čo znamená práve odvodený vzorec pre pravdepodobnosť? Vezmime si konkrétny prípad z predchádzajúceho príkladu. Keby sme robili filmový záznam plynu zo štyroch molekúl, zistili by sme, že v priemere každý 16 snímok by znázorňoval plyn v konfigurácii, keď sú všetky molekuly vľavo.
Ďalej by sme v priemere na každom štvrtom snímku mali vidieť jednu molekulu vľavo a tri vpravo. V priemere na 3/8 snímkov by bol počet molekúl v oboch častiach rovnaký.
Kvôli symetrii medzi ľavou a pravou časťou (obe časti sú rovnocenné) musí zrejme platiť, že P(n) = P(N – n), t.j. pravdepodobnosť, že v ľavej polovici bude n molekúl je rovnaká, ako pravdepodobnosť, že n molekúl bude v pravej polovici (čo znamená, že v ľavej polovici by bolo N – n molekúl). Táto vlastnosť vyplýva aj z vlastností kombinačných čísel.
Počítačový model plynu
Prichádza rad na vás! Na nasledujúcom Java applete si budete môcť overiť niektoré myšlienky z práve prebranej teórie. Java applet simuluje správanie sa sústavy dokonale tvrdých gulí, ktoré sú v beztiažovom stave uväznené v nádobe tvaru kocky. Každá guľa sa pohybuje medzi zrážkami s ostatnými guľami a zo stenou po priamke. Tieto zrážky sú dokonale pružné. Applet po spustení zobrazuje pohyb takejto sústavy gulí (molekúl).
Na nasledujúcich úlohách sa budete môcť sami presvedčiť, že veci sa majú tak, ako sme o nich písali v teórii.
|
Úloha A1 - Zoznámte sa! Applet predstavuje trojrozmerný model plynu. Ak chcete získať lepšiu predstavu o priestorovom rozložení molekúl v kocke, zájdite myšou nad applet a ťahajte so stlačeným ľavým tlačítkom tak, akoby ste chceli kocku otočiť. Tým zmeníte uhol pohľadu na plyn. Odporúčame potom, čo si túto možnosť vyskúšate, vrátiť kocku do pôvodnej polohy. Ak ste zabudli aká poloha to bola, kliknite na tlačítko REFRESH v hornej lište vášho internetového prezerača. Kliknite teraz na odkaz ŠTART tesne pod appletom v kolónke SIMULÁCIA. Molekuly v nádobe (je ich 40) sa dajú do pohybu. Sledujte chvíľku tento pohyb. Všímajte si, či sa počet molekúl v ľavej časti mení alebo nemení. Odhadnite: Mení sa veľmi? Simuláciu môžete kedykoľvek prerušiť kliknutím na odkaz STOP a potom ju znovu spustiť kliknutím na ŠTART. Spustite teraz simuláciu a v kolónke VYKRESĽOVANIE kliknite na odkaz ZÁVISLOSŤ n(t). Applet začne vykresľovať graf závislosti počtu molekúl v ľavej polovici n od času, presnejšie od poradového čísla políčka filmu j, ktorý z nášho plynu filmujeme fiktívnou kamerou (spomínali sme ju v teórii). Z tohoto grafu môžete ľahko vidieť, že sa počet molekúl v ľavej časti mení a že fluktuuje okolo strednej hodnoty 20. Ak chcete, aby applet znovu zobrazoval molekuly, kliknite na odkaz MOLEKULY v kolónke VYKRESĽOVANIE. Pod appletom môžete nastaviť aj iný počet molekúl. Do textového políčka napíšte nový počet (napr. 4) a stlačte tlačítko NASTAV. Skúste si to! S ostatnými ovládacími prvkami sa zoznámime neskôr, keď ich budeme potrebovať. |
Keď už viete ako applet ovládať, dáme sa do reálnej fyzikálnej práce. Zistíme, aké sú početnosti výskytov jednotlivých konfigurácií.
|
Úloha A2 – Experimentálne početnosti jednotlivých konfigurácií Naším cieľom bude teraz urobiť skutočné meranie početností výskytu jednotlivých konfigurácií v plyne pozostávajúcom z 10 molekúl. Ako cieľ dosiahneme? Zhruba takto: Necháme applet chvíľu bežať a potom z neho "vytiahneme" potrebné údaje, z ktorých zistíme, na koľkých políčkach fiktívneho filmu sa nachádzalo 0, 1, 2, 3, 4, ..., 10 molekúl. Tie potom spracujeme v Exceli. Poďme teda na to! Nastavte počet molekúl na 10 a spustite simuláciu. Prepnite sa do zobrazenia závislosti n(t) počtu molekúl v ľavej časti na čase. Počkajte, kým fiktívna kamera nenafotí aspoň 1100 snímkov. Potom simuláciu zastavte. Na grafe je zaznamenaný počet n molekúl v ľavej časti pre posledných 1024 políčok filmu. Ako teraz získať z appletu numerické údaje? Jednoducho! Pod appletom stlačte odkaz VYPÍŠ POČTY MOLEKÚL VĽAVO. To textového poľa sa vypíše stĺpec 1024 číselných údajov, predstavujúcich počty molekúl v ľavej polovici na jednotlivých políčkach filmu. Kliknite myšou do textového poľa s výpisom. Objaví sa textový kurzor. Skopírujte obsah textového políčka do clipboardu (stlačte najprv kombináciu kláves CTRL+A a potom CTRL+C). Otvorte si program Microsoft Excel a preneste doň svoje údaje (v Exceli kliknite do niektorej bunky a stlačte kombináciu kláves CTRL+V). Dajte si vložené údaje v Exceli zoradiť podľa veľkosti. Tak sa vám bude ľahšie počítať. Spočítajte potom, koľko políčok obsahovalo vľavo 0 molekúl, 1 molekulu, 2 molekuly, 3 molekuly, ..., 10 molekúl. Zapíšte v Exceli svoje výsledky do tabuľky a znázornite si ich graficky pomocou histogramu (stĺpcového diagramu). Sú tieto počty v zhode s počtami predpovedanými teóriou? (Teoretické hodnoty získate podobne ako sme ich získali pre prípad N = 4). Zistili ste vákuum v ľavej časti približne na 1 políčku filmu? Jednu molekulu v ľavej polovici približne na 10 políčkach filmu? Rovnomerné rozdelenie molekúl približne na 252 políčkach? Ak áno, získali ste výsledky predpovedané teóriou. Ak nie, vami získané hodnoty sa pravdepodobne od predpovedaných príliš nelíšia. Keďže je v hre náhoda, nie je možné zaručiť, že získate teoretické počty. Ale ak by ste ten istý pokus vykonali mnohokrát, v priemere by ste museli získať počty predpovedané teóriou. |
V ďalšej úlohe preskúmate, ako závisí veľkosť fluktuácií na počte molekúl plynu.
|
Úloha A3 – Veľkosť fluktuácií a počet častíc Preskúmame teraz časový vývoj plynu pozostávajúceho zo 40 molekúl. Nastavte v applete nový počet molekúl na 40. Spustite simuláciu. Sledujte časovú závislosť počtu molekúl v ľavej časti. Keď applet dôjde po 1200. políčko, simuláciu zastavte a vypíšte tak ako v predchádzajúcej úlohe počty molekúl vľavo na posledných 1024 políčkach. Prekopírujte ich do Excelu a vytvorte tabuľku početností jednotlivých možných konfigurácií. Svoje výsledky znázornite graficky pomocou histogramu (stĺpcového diagramu). Na histograme z úlohy A2 aj na terajšom histograme vytvárajú jednotlivé stĺpce kopec. Ktorý z histogramov má tento kopec relatívne "užší"? Relatívnou šírkou kopca rozumieme pomer šírky kopca a šírky celého histogramu. V ktorom prípade (N = 10 alebo N = 40) sú fluktuácie zreteľnejšie? Vzniklo vo vašom experimente s N = 40 v ľavej časti nádoby niekedy vákuum? Koľko políčok filmu by ste museli nafotiť, aby ste našli v priemere 1 políčko s n = 0? |
|
Úloha A4* – Predpovedzte veľkosť fluktuácií! Táto úloha je náročnejšia ako ostatné a preto je označená hviezdičkou. Ak sa vám bude zdať náročná. môžete ju pokojne vynechať. Majme plyn z 40 molekúl. Nájdite výpočtom také hodnoty nmin a nmax počtov molekúl v ľavej polovici, ktoré spĺňajú vlastnosť, že počet molekúl v ľavej polovici, n, bude nadobúdať s pravdepodobnosťou najviac 0,95 hodnoty spĺňajúce podmienku nmin Ł n Ł nmax Z hodnôt nmin a nmax potom určte šírku kopca na histograme početností výskytu jednotlivých hodnôt n z predchádzajúcej úlohy. Pozrite sa na hodnoty veličiny n, ktoré ste získali z appletu v predchádzajúcej úlohe a zistite, či sú často menšie ako nmin alebo väčšie ako nmax. |
V predchádzajúcich úlohách na applete sme videli, že stavy plynu, v ktorých je rozdelenie molekúl medzi polovice také nerovnomerné, že n << N/2, prípadne n >> N/2 zodpovedajú relatívne malému počtu konfigurácií. Takéto stavy, ktoré sa dajú získať len relatívne malým počtom spôsobov sú dosť špeciálne a preto sa nazývajú relatívne nenáhodné alebo usporiadané.
Na druhej strane tie stavy plynu, v ktorých je rozdelenie molekúl skoro rovnomerné (n » n') zodpovedajú mnohým možným konfiguráciám. Takéto stavy, ktoré možno získať mnohými rôznymi spôsobmi, sa nazývajú náhodné alebo neusporiadané.
Môžeme teda zhrnúť, že náhodnejšie (rovnomernejšie) rozdelenia molekúl plynu nastávajú častejšie ako menej náhodné rozdelenia.
Teraz sa pozrieme na to, aká je v skutočnosti pravdepodobnosť toho, že v ľavej polovici nádoby s plynom pozostávajúcim z N molekúl vznikne vákuum. Využijeme to, že existuje jediná konfigurácia, ktorá zodpovedá takémuto stavu plynu. Pravdepodobnosť nájdenia vákua potom bude
![]()
Pre plyn z 40 molekúl je táto pravdepodobnosť P(0) = 9,1.10–13. To, že v našom applete vznikne takýto stav samovoľne je veľmi nepravdepodobné. V priemere pripadá jedno políčko filmu, na ktorom by bol takýto stav zachytený na 1,1.1012 políčok filmu. Samozrejme tento jav nie je vylúčený. Je len nepravdepodobný.
Keď ste na applete modelovali plyn z 10 molekúl, bola pravdepodobnosť P(0) väčšia, konkrétne 1/1024. To znamená, že v priemere na jednom z 1024 políčok filmu by bol zachytený stav plynu s vákuom v ľavej polovici. Keď ste sa hrali s appletom, mohli ste sa s takýmto javom stretnúť.
Ako je to v bežnom živote? Uvažujme bežnú miestnosť s rozmermi 4m x 4m x 2,5m. Takáto miestnosť obsahuje za bežných podmienok zhruba 1027 molekúl. Aká je pravdepodobnosť, že v jej jednej polovici vznikne samovoľne vákuum?
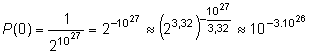
Číslo, ktoré sme dostali je dosť malé. Dalo by sa zapísať ako 0,00000 ....c..., kde c by bola prvá nenulová číslica, ktorá by sa nachádzala v čísle po 3.1026 nulách. Keby sme takéto číslo chceli napísať na papier, a šírka jednej nuly by bola 3 mm, bola by jeho dĺžka zhruba 9.1023 metrov, čo je asi 95 miliónov svetelných rokov. Keby ste na začiatku tohto čísla umiestnili baterku a zasvietili smerom k jeho koncu, signál by dorazil po 95 miliónoch rokov!
Samovoľný vznik vákua v polovici bežnej miestnosti možno preto prakticky považovať za nemožný, i keď prísne vzaté, je možný, len veľmi málo pravdepodobný.
Podobne málo pravdepodobné by boli aj stavy plynu, v ktorých by bolo v jednej polovici miestnosti len zopár molekúl. To nás vedie k nasledujúcemu všeobecnému záveru:
|
Ak je celkový počet častíc veľký, fluktuácie, ktoré zodpovedajú výrazne nerovnomerným rozdeleniam týchto molekúl, nenastávajú skoro nikdy. |
Môžeme to zapísať aj s troškou matematiky. Ak veľkosť fluktuácie označíme ako Dn, môžeme ju vypočítať ako
Dn = n – N/2
Keď je počet molekúl plynu N veľký, vyskytujú sa v jeho vývoji s významnou početnosťou iba také stavy, pre ktoré platí |Dn| << N. Ostatné stavy sa skoro vôbec nevyskytujú.
Plyn možno najdetailnejšie popísať vtedy, keď v každom čase udáme jeho mikrostav, t.j. keď budeme v každom čase poznať polohy a rýchlosti všetkých jeho molekúl. Z tohto pohľadu vyzerá časový vývoj molekúl plynu veľmi zložito, lebo molekuly navzájom interagujú a menia svoje polohy a rýchlosti, navonok veľmi zložitým spôsobom.
Z makroskopického hľadiska sa však nezaujímame o to, čo sa deje s jednotlivými molekulami plynu. Stačí nám menej podrobný popis plynu. Makrostav plynu možno popísať napríklad tak, že v každom čase udáme iba počet molekúl plynu v ľavej časti nádoby. Z takéhoto makroskopického pohľadu je izolovaná sústava s plynom, ktorá bola ponechaná sama na seba po dostatočne dlhú dobu, veľmi jednoduchý objekt, keďže nemá tendenciu sa v čase meniť.
Čo myslíme pod tým, že nemá tendenciu meniť sa? Predstavme si, že v nejakom čase t1 začneme filmovať plyn a budeme to robiť po nejakú rozumne dlhú dobu t. Neskôr, v čase t2 natočíme ďalší film z toho istého plynu, ktorý bude trvať presne tú istú dobu t. Z makroskopického hľadiska by tieto dva natočené filmy vyzerali zvyčajne rovnako. V oboch prípadoch by počet častíc v ľavej polovici nádoby n fluktuoval okolo tej istej hodnoty N/2, pričom veľkosť fluktuácií by v oboch prípadoch bola zvyčajne rovnaká. Ak zanedbáme veľmi zriedkavé prípady (o ktorých si pohovoríme o chvíľu) bude pozorovaný makrostav plynu nezávislý na začiatočnom čase nášho pozorovania. Presnejšie, hodnota, okolo ktorej n fluktuuje, sa v čase nebude meniť. Hovoríme, že plyn sa nachádza v rovnovážnom stave.
Nevratnosť
Predstavme si, že by sa stalo to, že všetky molekuly v plyne by sa zoskupili v ľavej polovici nádoby. Z predchádzajúceho už viete, že to, že niečo také samovoľne nastane. je úžasne nepravdepodobné, ale možné. To však neznamená, že plyn sa v takomto stave nemôže nachádzať. Mohli sme ho v takomto stave pripraviť, napríklad tak, že by sme ho nejakým piestom najprv stlačili do ľavej polovice nádoby a potom by sme piest rýchlo odstránili.
Nezávisle na tom, ako sa všetky molekuly dostali do ľavej časti nádoby (či už samovoľne alebo naším pričinením), vynára sa otázka, ako by sa molekuly ďalej správali. Zostali by naďalej všetky v ľavej polovici? Alebo by rovnomerne vyplnili celú nádobu? Čo by ste čakali? Skúsime takúto situáciu simulovať na applete.
|
Úloha A5 – Na začiatku všetky molekuly vľavo Nastavte si počet molekúl na 40. Pod appletom, v kolónke NASTAVENIE ZAČIATOČNÝCH PODMIENOK zaškrtnite zaškrtávacie políčko VŠETKY MOLEKULY NA ZAČIATKU VĽAVO. V applete sa všetky molekuly premiestnia do ľavej polovice. Potom začnite simuláciu. Najprv pozorujte plyn v zobrazení MOLEKULY. Čo sa s molekulami stane? Je to to, čo ste očakávali? Všimnite si, ako vyzerá graf závislosti n(t). Ak vám jeho začiatok medzičasom utiekol, musíte zastaviť simuláciu, a stisnúť tlačítko NASTAV v nastavení počtu molekúl. Tak dosiahnete opätovné nastavenie začiatočného stavu. |
Z toho čo ste pozorovali môžeme teraz vyvodiť závery. Je zrejme omnoho pravdepodobnejšie, že molekuly plynu sa časom z ľavej polovice nádoby rozptýlia do celej nádoby a nezostanú navždy v ľavej polovici. Ak by tam mali zostať (mohli by) museli by sa všetky na začiatku pohybovať veľmi špeciálnym spôsobom. Ale najpravdepodobnejšie je, že sa tak na začiatku pohybovať nebudú. Časom sa rozptýlia do celej nádoby a počet molekúl v ľavej polovici bude znovu fluktuovať okolo rovnovážnej hodnoty N/2.
Začiatočné rozmiestnenie všetkých molekúl v ľavej polovici nádoby môžeme chápať ako výnimočne veľkú a zároveň tiež výnimočne nepravdepodobnú fluktuáciu plynu nachádzajúceho sa v rovnovážnom stave. Každá fluktuácia má tendenciu čoskoro zaniknúť, prípadne sa zmenšiť. Preto sa molekuly časom rozptýlia po celej nádobe.
|
Keď je izolovaná sústava v značne nenáhodnom, usporiadanom stave, bude sa (až na fluktuácie, ktoré pravdepodobne nebudú veľké) v čase vyvíjať tak, že dosiahne nakoniec svoj najnáhodnejší, najmenej usporiadaný rovnovážny stav. |
Doba zániku nerovnovážneho usporiadania molekúl (fluktuácie) sa nazýva relaxačný čas a môže byť krátky (mikrosekundy), ale aj dlhý (storočia). Všetko to závisí od mikroskopických vlastností častíc sústavy.
Z predchádzajúceho by malo byť jasné, že keď sa izolovaný makroskopický systém mení v čase, má tendenciu tak robiť veľmi určitým spôsobom, menovite z menej náhodného stavu do viac náhodného stavu (z usporiadanejšieho stavu do menej usporiadaného). Tento proces zmeny by sme mohli zaznamenať na filmový pás a potom si ho premietnuť na premietačke. Predpokladajme teraz, že by sme si zaznamenaný filmový pás pustili cez projektor v opačnom smere. Na plátne by sme potom pozorovali časovo-obrátený proces, t.j. proces, ktorý by prebehol, keby niekto zmenil smer behu času. Film na plátne by potom vyzeral naozaj veľmi svojrázne, keďže by zobrazoval proces, v ktorom sa systém mení z viac náhodného do omnoho menej náhodného stavu. Takéto niečo by v skutočnosti skoro vôbec nebolo možné pozorovať. Na základe toho, čo by sme pri premietaní takého filmu videli, by sme mohli skoro s úplnou istotou prehlásiť, že film sa premieta odzadu.
|
Príklad – Film beží odzadu! Predpokladajme, že máme sústavu 40 molekúl, ktoré sú na začiatku všetky v ľavej polovici nádoby. Nafilmujeme ich ďalší časový vývoj na filmový pás. Molekuly sa z ľavej polovice postupne rozptýlia do celej nádoby a vyplnia ju v podstate rovnomerne. Takýto proces sa nám zdá prirodzený. Ak by sme na druhej strane zaznamenaný film premietli odzadu, videli by sme, že plyn sa mení veľmi zvláštnym spôsobom. Na začiatku by bol rovnomerne rozptýlený v nádobe a po chvíli by sa spontánne skoncentroval v ľavej polovici, ponechajúc pravú polovicu prázdnu. Takýto proces sa v reálnom živote prakticky nikdy nevyskytuje. To neznamená, že by nemohol nastať. Znamená to len, že je totálne nepravdepodobný. To, čo znázorňuje spätne premietaný film by v skutočnosti mohlo nastať, ak by mali všetky molekuly plynu veľmi špeciálne polohy a rýchlosti. Ale to, aby takéto špeciálne polohy a rýchlosti mali, je neuveriteľne málo pravdepodobné. Pravdepodobnosť toho, že sa voľačo také stane je v skutočnosti rovnaká ako pravdepodobnosť vzniku fluktuácie pri ktorej n = N. Ak by sme teda na filmovom plátne niečo také pozorovali, mohli by sme skoro s istotou tvrdiť, že film beží odzadu. |
V nasledujúcej úlohe sa na applete pokúsite napodobiť takú nepravdepodobnú situáciu, v ktorej sa molekuly premiestnia z celej nádoby samé od seba všetky do jej ľavej časti. Ako niečo také dosiahnuť?
Odpoveď je veľmi jednoduchá! Stačí na začiatku umiestniť všetku molekuly do ľavej polovice nádoby a nechať ich vyvíjať sa v čase. Po chvíľke treba simuláciu zastaviť a zmeniť rýchlosti všetkých molekúl na opačné! Potom treba simuláciu znovu spustiť a sledovať, ako sa každá molekula vráti späť do ľavej polovice nádoby, presne po trajektórii, ktorou sa pohybovala predtým! Poďme teda na to!
|
Úloha A6 – Ako sa môže stať nemožné? Nastavte na applete počet molekúl na 40. Zaškrtnite zaškrtávacie políčko VŠETKY MOLEKULY NA ZAČIATKU VĽAVO. Zvoľte vykresľovanie časovej závislosti n(t) a spustite applet. Pozor! Nechajte ho bežať len krátko, približne dovtedy, pokým sa nenafotí okolo 30 políčok filmu. Potom applet zastavte. Kliknite na odkaz NASTAV OPAČNÉ RÝCHLOSTI. Applet zmení vektory rýchlosti všetkých molekúl na opačné. Prepnite sa do zobrazenia MOLEKULY, dobre sa usaďte a spustite znovu simuláciu. To, čo uvidíte, je veľmi výnimočný jav! Molekuly sa samé od seba skoncentrujú v ľavej polovici nádoby! Poznámka: Prečo sme požadovali, aby ste nechali na začiatku applet bežať len krátko (30 políčok filmu)? Odpoveď na túto otázku je zaujímavá. Počítač používa pri výpočtoch čísla typu double, t.j. počíta s presnosťou na asi 15 desatinných miest. Čím dlhšie simulácia beží, tým viac narastá numerická chyba výpočtu. Na to, aby sa plyn vrátil znovu do ľavej polovice nádoby, je potrebné s veľmi veľkou presnosťou nastaviť vhodné polohy a rýchlosti molekúl. Potrebná presnosť je tým väčšia, čím dlhšie sme na začiatku nechali applet bežať. Presnosť, s ktorou počíta applet, mu postačí, aby sa plyn vedel vrátiť do ľavej polovice po tridsiatich nafotených políčkach. Nestačí však už napríklad na 100 a viac políčok. Skúste si to! |
O nejakom procese budeme hovoriť, že to je nevratný proces, ak k nemu prislúchajúci časovo-obrátený proces nastáva v skutočnosti len s mizivou pravdepodobnosťou. Všetky makroskopické systémy, ktoré nie sú v stave rovnováhy, majú tendenciu dosiahnuť rovnováhu, t.j. situáciu s najväčšou náhodnosťou. Teda vidíme, že všetky takéto systémy sa správajú nevratne. Keďže sme v bežnom živote neustále obklopení systémami, ktoré nie sú v stave rovnováhy, začína byť zrejmé, prečo má čas jednoznačný smer, ktorý nám umožňuje jasne rozlíšiť minulosť od budúcnosti.
Predstavme si, že by niekto natáčal na film padajúci dážď. Kvapky dažďa by padali na zem a vytvárali by postupne mláku. Keby sme si takýto film pustili odzadu, videli by sme, ako sú z mláky vystreľované nahor jednotlivé kvapky dažďa a ako miznú hore v oblakoch. Takéto niečo nie je síce podľa zákonov fyziky vylúčené, ale je to úplne nepravdepodobné. Ak by sme niekedy niečo také naozaj videli (napríklad v televízii), môžeme znovu takmer s istotou tvrdiť, že sa film premieta odzadu, späť v čase. V tomto zmysle je smer času jednoznačný. Je oveľa pravdepodobnejšie, že sa kinetická energia padajúcej kvapky rozdelí medzi miliardy molekúl vody v mláke, ako že nastane opačný jav, v ktorom by sa niektoré molekuly mláky museli pohybovať veľmi špeciálnym spôsobom, aby sa ich rýchlosť výrazne zvýšila a smerovala nahor a aby vytvorili kvapku, ktorá by bola vymrštená zvislo nahor.
Na nasledujúcom obrázku je to, čo sme doteraz povedali o nevratných procesoch znázornené so štipkou humoru. Udalosti na obrázku by sa mohli stať v časovej postupnosti na obrázku, ale je to extrémne nepravdepodobné.

Fluktuácie a každodenný život
Mohlo by to vyzerať tak, že všetko, čo sme doteraz povedali o fluktuáciách je teoretickou záležitosťou a v praxi sa s fluktuáciami nestretneme. Opak je pravdou. Uvedieme dva prípady, ktoré budú ilustrovať všadeprítomnosť fluktuácií.
Fluktuácie hustoty vzduchu a farba oblohy
Ak je počet molekúl vzduchu v nádobe veľký, fluktuácie sú relatívne veľmi malé. Ak je však molekúl málo, fluktuácie sú omnoho výraznejšie. Sú to práve fluktuácie hustoty vzduchu, ktoré spôsobujú modrú farbu oblohy. Keby nebolo ich, bola by obloha počas dňa čierna.
Keby bola hustota vzduchu konštantná, predstavoval by vzduch homogénne optické prostredie s konštantným indexom lomu a svetlo by sa v ňom šírilo po priamkach. V skutočnosti sa svetlo nešíri priamočiaro, ale rozptyľuje sa na fluktuáciách hustoty vzduchu. Predstavme si, že celú atmosféru rozdelíme na malé myslené kocôčky s hranou veľkosti vlnovej dĺžky svetla (zhruba 5.10 – 7 m). Za bežných podmienok je počet molekúl v každej z takých kocôčok zhruba 3 milióny, čo je strašne málo. Počet molekúl v kocôčkach sa bude neustále meniť, keďže z každej kocôčky nejaké molekuly odchádzajú a nejaké do nej prichádzajú. Vzniknú teda fluktuácie počtu molekúl v kocôčkach a teda aj hustoty vzduchu v každej z kocôčok. Mierne odlišná hustota vzduchu znamená mierne odlišný index lomu a ten vedie k rozptylu svetla. Lepšie sa rozptyľujú kratšie vlnové dĺžky ako dlhšie a preto víťazí modrá farba. Obloha je modrá!
Fluktuácie napätia na rezistore - šum
Keď napojíme rezistor na zosilňovač elektrického napätia a výstup z neho pripojíme na citlivý osciloskop, zistíme, že signál na osciloskope nebude nulový, ale že napätie zobrazované osciloskopom bude neustále náhodne a neusporiadane kmitať okolo nulovej strednej hodnoty. Inžinier vám povie, že osciloskop zaznamenáva šum. Čo je však zdrojom tohto šumu?
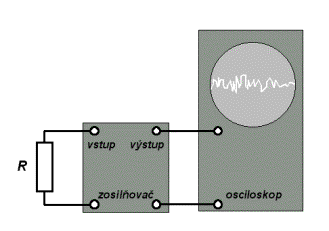
Rezistor je kovový vodič, ktorý má vo svojom vnútri obrovské množstvo voľných elektrónov, ktoré sa môžu pohybovať (podobne ako molekuly plynu) po celom rezistore. Týmto elektrónom sa hovorí vodivostné elektróny, lebo sprostredkúvajú vedenie elektrického prúdu v rezistore. Vďaka tomu, že sa tieto elektróny správajú podobne ako plyn, nie je ťažké uhádnuť zdroj šumu na osciloskope! Počet vodivostných elektrónov v ľavej a pravej časti rezistora bude neustále fluktuovať okolo strednej hodnoty. To znamená, že sa môže bežne stať, že v jednej polovici rezistora je viac elektrónov ako v druhej. To znamená, že náboj tejto polovice bude zápornejší ako náboj tej druhej a medzi oboma polovicami vznikne elektrické napätie. Toto napätie bude raz kladné a raz záporne. Bude sa navyše neustále meniť. Takto vzniká šum. Na nasledujúcom obrázku je ukážka toho ako vyzerá priebeh signálu na osciloskope v takomto experimente.
Lahôdka na záver
Na úplný záver sme si pre vás nechali lahôdku. Uvádzame úryvok z vedecko-populárnej knihy Pán Tompkins stále v říši divů. Jedna z hlavných postáv knihy Maud, manželka pána Tompkinsa, sa zmenší skoro na veľkosť molekúl a je doprevádzaná Maxwellovým Démonom po pohári s whisky. Na jej manžela a jej otca, profesora fyziky, čaká čosi veľmi zaujímavé . . .
|
Maxwellov Démon potom Maud odviedol priamo k povrchu kvapaliny. Teraz uvidela veľké priehľadné kocky tvorené nespočetnými molekulami, ktoré boli úhľadne usporiadané jedna vedľa druhej ako tehly v múre. Ich rovný a hladký povrch vystupoval z povrchu whiskového mora. "To je úžasné!" vzdychla Maud. "Vyzerá to ako zasklená budova plná kancelárií!" "To nie je sklo, ale ľad," opravil ju Démon. "Vidíte časť kryštálu ľadu jednej z kociek v otcovom pohári. Keby ste sa na chvíľu posadili," požiadal ju, "mám teraz nejaké povinnosti." Usadil Maud na kraj jedného z kryštálov ľadu, kde sa krčila ako horolezec, ktorý prepäl svoje sily. Maxwellov Démon potom vyzbrojený nástrojom podobným tenisovej rakete skočil do whiskového mora. Maud ho sledovala, ako pláva a rozdáva rany molekulám navôkol. Vrhal sa tu jedným, tam druhým smerom, a niektoré molekuly usmerňoval na jednu stranu, iné na opačnú. Spočiatku vôbec nechápala, či má jeho konanie nejakú logiku, ale potom jej začal byť jeho zámer jasný: Démon oddeľoval rýchle a pomalé molekuly a posielal ich na opačné strany. Maud musela obdivovať, s akou rýchlosťou a obratnosťou si počína. Tá úžasná rýchlosť, s ktorou sa orientoval! Tá obratnosť! Od tohto chlapíka by sa mohli wimbledonskí šampióni všeličo priučiť. Po krátkej chvíli bol výsledok Démonovej práce zrejmý. Polovica povrchu kvapaliny bola teraz pokrytá pomalými molekulami, zatiaľ čo molekuly v druhej polovici sa pohybovali čím ďalej, tým divokejšie. Počet molekúl, ktoré unikali z povrchu pri procese vyparovania, sa rýchlo zväčšoval. V zhlukoch po tisíckach sa predierali povrchom v podobe veľkých bublín a vyskakovali von. Bolo ich toľko, že Maud len sem tam cez zástupy zbláznených molekúl zahliadla mihnutie Démonovej rakety alebo cíp jeho smokingu. Náhle stál Démon vedľa nej. "Rýchlo," povedal, "je čas odtiaľ zmiznúť, lebo nás to oparí."
S týmito slovami ju znovu pevne vzal za ruku a unášal ju nahor. Zastavili sa vysoko nad verandou a Maud pozorovala pod sebou manžela s otcom. Otec náhle vyskočil. "Dobrotivý Bože!" vykríkol a s úžasom hľadel na pohár s whisky. "Ono to vrie!" A naozaj. Whisky v pohári bola pokrytá praskajúcimi bublinami a stúpala z nej para. "Vidíš to!" šepkal profesor obdivným, pohnutým hlasom. "Práve som ti rozprával o zákone entropie a štatistických fluktuáciách — a teraz jednu takú fluktuáciu vidíme! Nejakou neuveriteľnou zhodou okolností, možno že po prvý krát v celej histórii Zeme, sa rýchle molekuly náhodou nahromadili v jednej časti povrchu vody a tá začala sama od seba vrieť! Prejdú miliardy rokov a my budeme pravdepodobne jedinými ľuďmi, ktorí mali príležitosť uvidieť tak mimoriadny jav. Aké neuveriteľné šťastie!" |