F. Teória interferencie svetla na tenkej vrstve

OBSAH:

Najkrajšie javy vznikajú vtedy, keď svetlo dopadá na tenkú vrstvu látky s nejakým indexom lomu obklopenej z oboch strán prostrediami s inými indexmi lomu. Príkladom takejto tenkej vrstvy môže byť bublina. Ak na bublinu dopadá biele svetlo, vidíme na nej nádherné dúhové farby. Podobné farby vidíme aj vtedy, keď biele svetlo dopadá na tenučkú vrstvičku oleja rozliateho na povrchu mláky, ktorý tam vytiekol z nejakého auta.

Závislosť vlnovej dĺžky na indexe lomu
Pre začiatok preskúmame. čo sa udeje s monochromatickým svetlom s nejakou danou vlnovou dĺžkou, keď dopadne z vákua do optického prostredia s indexom lomu n.

Na predchádzajúcom applete ste zistili, že vlnová dĺžka svetelnej vlny a aj jej rýchlosť závisia na prostredí, ktorým sa vlna šíri. Čím je dané optické prostredie opticky hustejšie, tým je vlna kratšia. Sami ste si pravdepodobne vytvorili hypotézu, že vlnová dĺžka vlny v optickom prostredí s indexom lomu n je n-krát kratšia ako vo vákuu.

Tento jav súvisí s tým, že perióda vlny musí byť vo vákuu aj v danom optickom prostredí rovnaká. Teraz si ho vysvetlíme.

Označme T₀ periódu svetelnej vlny vo vákuu a T periódu svetelnej vlny v optickom prostredí s indexom lomu n. Nech ₀ je vlnová dĺžka vlny vo vákuu a jej vlnová dĺžka v optickom prostredí s indexom lomu n. Rýchlosť svetelnej vlny vo vákuu je c, zatiaľ čo v optickom prostredí má menšiu rýchlosť

Keďže perióda svetelnej vlny musí byť vo vákuu aj v optickom prostredí rovnaká, bude platiť:

Keďže vlnovú dĺžku ľubovoľnej vlny vyjadríme ako , kde v je rýchlosť vlny a T je jej perióda, môžeme písať:

Z toho po úprave dostávame:

To znamená, že svetelná vlna, ktorá má vo vákuu vlnovú dĺžku ₀, bude mať v prostredí s indexom lomu n vlnovú dĺžku n-krát menšiu.

Interferencia svetla na tenkej vzduchovej vrstve
Teraz sa sústredíme na to, čo sa udeje so svetelnou vlnou, keď dopadne zo skla s indexom lomu n na tenkú vzduchovú vrstvu s hrúbkou d. Situáciu výstižne popisuje nasledujúci obrázok.

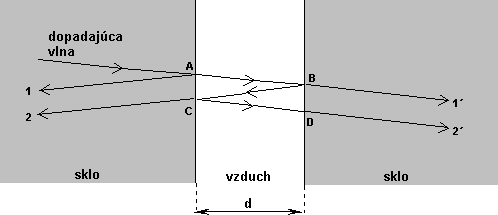
Predpokladajme, že kolmo na tenkú vzduchovú vrstvu medzi dvoma kusmi skla s rovinnými povrchmi dopadá zo skla svetelná vlna. Kvôli prehľadnosti dopadá svetelná vlna na obrázku na vrstvu vzduchu skoro kolmo. Dopadne v bode A, kde sa vlna rozdelí. Jedna jej časť (vlna 1) sa odrazí, pričom, keďže sa odráža na opticky redšom prostredí, nezmení fázu na opačnú. Druhá časť dopadajúcej vlny pokračuje bez zmeny fázy cez tenkú vrstvu z bodu A do bodu B.

V bode B dopadá na rozhranie a znovu sa rozdelí. Jedna jej časť letí so zmenou fázy na opačnú z bodu B do C (odraz na opticky hustejšom prostredí) a druhá jej časť prechádza bez zmeny fázy do skla (vlna 1´).

Vlna ktorá letela z bodu B do C dopadne v bode C na rozhranie a znovu sa rozdelí. Jedna jej časť prejde bez zmeny fázy do skla (vlna 2) a druhá jej časť sa odrazí na rozhraní, pričom zmení fázu na opačnú (odraz na opticky redšom prostredí) a prejde z C do D. Vlna ktorá dopadá z C do D sa v D v skutočnosti znovu rozdelí. Toto rozdelenie však teraz nebudeme uvažovať. Budeme predpokladať, že celá táto vlna prechádza bez zmeny fázy do skla (vlna 2´).

Výsledné vlnenie v odrazenom svetle
Všimneme si teraz vlny 1 a 2, ktoré sa vracajú od vrstvičky vzduchu. Vlna 1 vznikla priamo z dopadajúceho vlnenia na prvom povrchu. Na to, aby z dopadajúceho vlnenia vznikla vlna 2, musí dopadajúce vlnenie prejsť dvakrát vzdialenosť d. Raz tam a raz späť. Medzi vlnou 2 a vlnou 1 teda bude existovať dráhový rozdiel, keďže dopadajúca vlna musí prejsť väčšiu dráhu aby vznikla vlna 2 ako keď má vzniknúť vlna 1. Keď počítame dráhový rozdiel medzi vlnami 1 a 2 musíme však ešte zobrať do úvahy fakt, že dopadajúca vlna zmenila v bode B fázu na opačnú, teda o 180°. Tomu zodpovedá dráhový rozdiel /2. Hodnota celkového dráhového rozdielu medzi vlnami 1 a 2 je preto 2d + /2.

Výsledné vlnenie v odrazenom svetle získame interferenciou vĺn 1 a 2. K zosilneniu vlnení dôjde, ak bude dráhový rozdiel párnym násobkom /2, teda ak

Toto sa ľahko dá upraviť na tvar

(1) [Najväčšie ZOSILNENIE v ODRAZENOM svetle]

K zoslabeniu vlnení dôjde ak bude ich dráhový rozdiel nepárnym násobkom /2, teda keď

Po úprave dostávame:

(2) [Najväčšie ZOSLABENIE v ODRAZENOM svetle]

Výsledné vlnenie v prejdenom svetle
Všimneme si teraz vlny 1´ a 2´, ktoré prešli vrstvičkou vzduchu. Vlna 1´ vznikla priamo z dopadajúceho vlnenia na druhom povrchu v bode B. Na to, aby z dopadajúceho vlnenia vznikla vlna 2´, musí dopadajúce vlnenie prejsť ešte dvakrát vzdialenosť d. Raz späť (BC) a raz znovu dopredu (CD). Medzi vlnou 2´ a vlnou 1´ teda bude existovať dráhový rozdiel, keďže dopadajúca vlna musí prejsť väčšiu dráhu aby vznikla vlna 2´ ako keď má vzniknúť vlna 1´. Keď počítame dráhový rozdiel medzi vlnami 1´ a 2´ musíme však ešte zobrať do úvahy fakt, že dopadajúca vlna zmenila v bodoch B a C fázu na opačnú, teda o 180°+180° = 360°. To je rovnaké, ako keby fázu vôbec nezmenila. Preto nemusíme brať do úvahy žiaden dráhový rozdiel. Hodnota celkového dráhového rozdielu medzi vlnami 1´ a 2´ je preto len 2d.

Výsledné vlnenie v prejdenom svetle získame interferenciou vĺn 1´ a 2´. K zosilneniu vlnení dôjde, ak bude dráhový rozdiel párnym násobkom /2, teda ak

Toto sa ľahko dá upraviť na tvar

(3) [Najväčšie ZOSILNENIE v PREJDENOM svetle]

K najväčšiemu zoslabeniu vlnení dôjde ak bude ich dráhový rozdiel nepárnym násobkom /2, teda keď

(4) [Najväčšie ZOSLABENIE v PREJDENOM svetle]

Z odvodených vzťahov je ľahké vidieť, že vtedy, keď sa zosilňuje na tenkej vrstve odrazené svetlo, prejdené svetlo sa zoslabuje. A naopak, keď sa zoslabuje odrazené svetlo, prejdené svetlo sa zosilňuje.

Prípad tenkej vrstvy z materiálu s indexom lomu n < n_sklo
Predpokladajme, že by sme medzi rovnobežnými sklennými doštičkami z predchádzajúcej úlohy mali namiesto vzduchu vodu. Situácia by sa veľmi nezmenila. Svetlo by znovu menilo fázu pri odraze v bode B a C.

Napíšme si pre zaujímavosť, akú hrúbku by vtedy mala mať vrstvička vody, aby sme dostali zoslabenie v odrazenom svetle (viď vzorec 2). Musíme len zobrať do úvahy fakt, že vlnová dĺžka svetla sa vo vode s indexom lomu n skráti n-krát. Vzorec (2) možno teda zapísať v tvare

kde sme namiesto dosadili /n.

To sa dá výhodnejšie zapísať v krajšom tvare

ktorý sa formálne podobá na vzorec (2) pre vzduchovú vrstvičku. Namiesto veličiny 2d, ktorá v prípade vzduchovej vrstvičky predstavovala dvojnásobok hrúbky vrstvy, máme teraz do činenia s veličinou 2nd.

Veličina nd sa nazýva optická hrúbka tenkej vrstvy. Veličina 2nd je preto dvojnásobok optickej hrúbky tenkej vrstvy.

Ak budeme počítať ľubovoľnú úlohu s tenkou vrstvou z materiálu s indexom lomu n, je pri výpočte dráhového rozdielu medzi rôznymi vlneniami nutné nahradiť hrúbku vrstvy d jej optickou hrúbkou nd. Tým zohľadníme to, že svetelné vlnenie sa v prostredí s indexom lomu n pohybuje pomalšie a má kratšiu vlnovú dĺžku.

To, čo sme sa tu naučili zaťiaľ len teoreticky si na nasldujúcej stránke overíme aj prakticky, v úlohách pre prácu s appletom Tenká vrstva.