Dandelinove dôkazy

V roku 1822 dokázal Germinal Pierre Dandelin veľmi elegantným spôsobom, že elipsa, parabola a hyperbola vznikajú ako prienik roviny a kužeľovej plochy. Jeho dôkaz využíva gule, ktoré sú vpísané do vnútra kužeľovej plochy a dotýkajú sa tiež roviny rezu. Body dotyku predstavujú ohniská kužeľosečky. V ďalšom uvádzame pre priateľov matematiky postupne všetky tri Dandelinove dôkazy.
Späť na applet

Dandelinov dôkaz pre elipsu
Zaškrtnite na applete kruhový volič ELIPSA. Zaškrtnite zaškrtávacie políčko KRESLIŤ DANDELINOVU KONŠTRUKCIU. Na obrázku sa objavia dve gule. Prvá má stred C a dotýka sa zvnútra kužeľa v dotykovej kružnici k a zhora sa dotýka roviny rezu v bode F. Druhá guľa má stred C', zvnútra sa dotýka kužeľa v dotykovej kružnici k' a zdola roviny rezu v bode F'. O bodoch F a F' o chvíľu ukážeme, že sú to ohniská elipsy. Myšou zájdite nad nejaký bod kužeľosečky. Bod sa pritom označí ako P a na obrázku sa okrem neho objavia úsečky PT a PT'. Pritom bod T je priesečníkom priamky PV a kružnice k, zatiaľ čo bod T' je priesečník priamky PV a kružnice k'. Sú to teda dotykové body, v ktorých sa priamka PV dotýka gulí vpísaných do kužeľa.

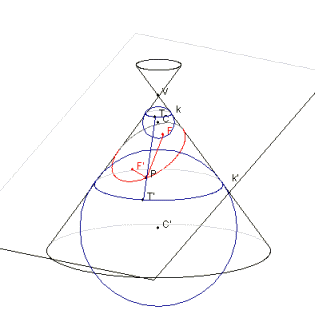
Teraz ukážeme, že krivka, ktorá vznikla ako prienik roviny rezu a kužeľovej plochy je elipsa. Uvažujme bod tejto krivky P. Ukážeme, že súčet jeho vzdialeností od bodov F a F' je konštantný. To bude znamenať, že skúmaná krivka je elipsa. Poďme teda na to!

(1) Platí, že |PF| = |PT|. Prečo? Aj bod F aj bod T ležia na dvoch dotykových priamkach vedených z bodu P ku hornej guli. Všetky takéto dotykové priamky z bodu P ku guli tvoria akúsi "kužeľovú čiapočku gule" pričom vzdialenosť všetkých bodov dotyku od bodu P je rovnaká. Preto sú rovnaké aj vzdialenosti |PF| a |PT|.

(2) Podobne platí, že |PF'| = |PT'|, lebo body F' aj T' ležia na dvoch dotykových priamkach vedených z bodu P ku spodnej guli so stredom C'.

(3) Keďže |PF| = |PT| a |PF'| = |PT'|, bude platiť, že |PF| + |PF'| = |PT| + |PT'|. Lenže body T, P a T' ležia na tej istej priamke VP prechádzajúcej vrcholom kužeľa, teda platí |PT| + |PT'| = |TT'|

Keď zvolíme pre bod P inú polohu na skúmanej krivke, dostaneme iné body T a T'. Dôležité však je, že vzdialenosť |TT'| bude tá istá, lebo predstavuje "najkratšiu vzdialenosť medzi dotykovými kružnicami k a k' po kužeľovej ploche". Teda skúmaná krivka je elipsa. QED.
Späť na applet

Dandelinov dôkaz pre hyperbolu
Zaškrtnite na applete kruhový volič HYPERBOLA. Zaškrtnite zaškrtávacie políčko KRESLIŤ DANDELINOVU KONŠTRUKCIU. Na obrázku sa objavia dve gule. Prvá má stred C pod bodom V a dotýka sa zvnútra kužeľa v dotykovej kružnici k a roviny rezu sa dotýka v bode F. Druhá guľa má stred C' nad bodom V, zvnútra sa dotýka kužeľa v dotykovej kružnici k' a roviny rezu v bode F'. O bodoch F a F' o chvíľu ukážeme, že sú to ohniská hyperboly. Myšou zájdite nad nejaký bod kužeľosečky. Bod sa pritom označí ako P a na obrázku sa okrem neho objavia úsečky PT a PT'. Pritom bod T je priesečníkom priamky PV a kružnice k, zatiaľ čo bod T' je priesečník priamky PV a kružnice k'. Sú to teda dotykové body, v ktorých sa priamka PV dotýka gulí vpísaných do kužeľa.

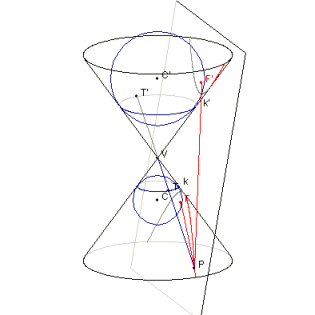
Teraz ukážeme, že krivka, ktorá vznikla ako prienik roviny rezu a kužeľovej plochy je hyperbola. Uvažujme bod tejto krivky P, ležiaci na jej spodnej vetve. Ukážeme, že rozdiel jeho vzdialeností od bodov F' a F je konštantný. To bude znamenať, že skúmaná krivka je hyperbola. Začnime!

Podobne ako v prípade elipsy platí, že |PF| = |PT| a |PF'| = |PT'|. Preto bude platiť, že |PF'| – |PF| = |PT'| – |PT|. Lenže body T, P a T' znovu ležia na tej istej priamke VP prechádzajúcej vrcholom kužeľa, ale tentoraz na opačných stranách bodu V. Teda platí |PT'| – |PT| = |T'T|

Keď zvolíme pre bod P inú polohu na spodnej vetve skúmanej krivky, dostaneme iné body T a T'. Ale vzdialenosť |T'T| bude tá istá, lebo predstavuje "najkratšiu vzdialenosť medzi dotykovými kružnicami k a k' po kužeľovej ploche". Podobne by sme postupovali pre bod P na hornej vetve skúmanej krivky, akurát by sme skúmali rozdiel vzdialeností |PF| – |PF'|. Došli by sme k rovnakým záverom. Teda skúmaná krivka je hyperbola. QED.
Späť na applet

Dandelinov dôkaz pre parabolu
Zaškrtnite na applete kruhový volič PARABOLA. Zaškrtnite zaškrtávacie políčko KRESLIŤ DANDELINOVU KONŠTRUKCIU. Na obrázku sa objaví teraz len jedna guľa. Má stred C pod bodom V a dotýka sa zvnútra kužeľa v dotykovej kružnici k a roviny rezu sa dotýka v bode F. Okrem roviny rezu sa na obrázku objaví aj rovina, v ktorej leží dotyková kružnica k. Prienikom tejto roviny a roviny rezu je priamka p. O bode F o chvíľu ukážeme, že je ohniskom paraboly a o priamke p ukážeme, že je jej riadiacou priamkou. Myšou zájdite nad nejaký bod kužeľosečky. Bod sa pritom označí ako P a na obrázku sa okrem neho objavia body T, Q, S a ich spájajúce úsečky. Pritom bod T je priesečníkom priamky PV a kružnice k. Bod Q je kolmým priemetom bodu P do roviny kružnice k. Bod S je pätou kolmice vedenej z bodu P na priamku p.

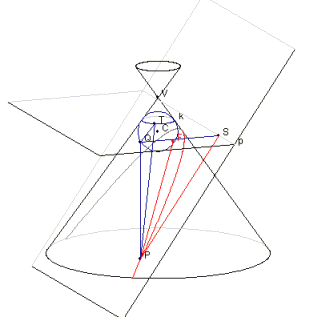
Teraz ukážeme, že krivka, ktorá vznikla ako prienik roviny rezu a kužeľovej plochy je parabola. Uvažujme bod tejto krivky P. Ukážeme, že jeho vzdialenosť od bodu F je rovnaká ako jeho vzdialenosť od priamky p. To bude znamenať, že skúmaná krivka je parabola.

Tak ako v prípade elipsy aj hyperboly, aj teraz platí, že |PF| = |PT|. Stačí teda ukázať, že |PT| = |PS|. Úsečky PT a PS sú obe preponami pravouhlých trojuholníkov PQT a PQS. Tieto dva pravouhlé trojuholníky sú podľa vety (usu) zhodné, lebo sa zhodujú v jednej strane PQ a v dvoch uhloch. Majú zhodné pravé uhly a zhodné sú aj uhly PTQ a PSQ. (Prečo sú posledné dva uhly zhodné? Na to, aby nám ako prienik roviny a kužeľovej plochy vznika parabola, je potrebné aby zvierala rovina rezu s rovinou podstavy kužeľa rovnaký uhol ako akákoľvek priamka kužeľa prechádzajúca jeho vrcholom. Uhly PTQ a PSQ sa tomuto uhlu rovnajú.)

Ak teda zhrnieme: |PF| = |PT| = |PS| = |P,p|. Teda vzdialenosť bodu P skúmanej krivky od bodu F sa rovná jeho vzdialenosti od priamky p. QED
Späť na applet