A. Definície kužeľosečiek

OBSAH:

Pripomeňme si najprv, čo rozumieme pod elipsou, čo pod hyperbolou a čo pod parabolou.

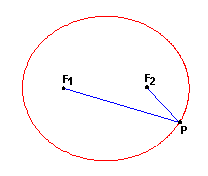
Elipsou nazývame množinu všetkých bodov P roviny, ktoré majú od dvoch daných pevných bodov tejto roviny F₁, F₂ (ohnísk) konštantný súčet vzdialeností, t.j. platí pre ne, že |F₁P| + |PF₂| = 2a > |F₁F₂|, kde 2a je konštanta, väčšia ako je vzdialenosť ohnísk.

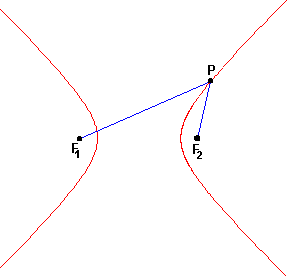
Hyperbolou nazývame množinu všetkých bodov P roviny, ktoré majú od dvoch daných pevných bodov tejto roviny F₁, F₂ (ohnísk) konštantnú absolútnu hodnotu rozdielu vzdialeností, t.j. platí pre ne, že | |F₁P| – |PF₂| | = 2a < |F₁F₂|, pričom 2a je konštanta, menšia ako je vzdialenosť ohnísk. Hyperbola sa skladá z dvoch vetiev. Pre body P na jednej z nich platí |F₁P| – |PF₂| = 2a, pre body P na druhej z nich platí |F₂P| – |PF₁| = 2a.

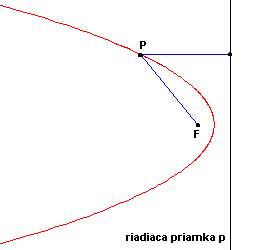
Parabolou nazývame množinu všetkých bodov P roviny, ktoré majú od danej pevnej priamky p tejto roviny, a od daného pevného bodu F tejto roviny (ohniska), neležiaceho na priamke p, rovnakú vzdialenosť, t.j. platí pre ne, že |FP| = |Pp| .