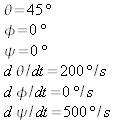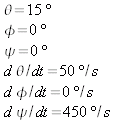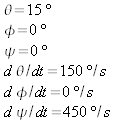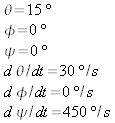OBSAH:
Úvod
A.
Úryvok, ktorým to všetko začalo
B.
Učebný text
C.
Model taniera
D.
Odkazy
|
Na tejto stránke sa nachádza interaktívny model taniera vyhodeného do vzduchu. Tento model vám umožní pre rôzne začiatočné podmienky sledovať pohyb taniera (a iných telies). Okrem toho sa pod modelom nachádzajú tzv. bádania. Sú to fyzikálne úlohy výskumného charakteru, pri ktorých riešení budete musieť využiť interaktívny model taniera.
|
Úvod
V
učebnom texte si prečítajte Kapitolu 3, Teoretický popis
pohybu taniera. Potom sa riaďte
nasledujúcimi pokynmi.
Na applete stlačte tlačidlo ĎALEJ, čím naštartujete model taniera. Po
stlačení tlačidla sa pred vami objaví tanier. V menu POMOC si zvoľte
položku POMOC a podrobne si prečítajte pokyny k ovládaniu appletu!
(Ešte raz si prečítajte poslednú vetu a vezmite ju vážne! Prečítaním
pomoci sa dozviete dôležité fakty, na ktoré sami nemôžete
prísť.)
Späť na applet ...
|
|
Bádanie 1 - Určujeme mierky
Určite ste si v pomoci prečítali informácie o tom, v akých jednotkách
sa v applete meria poloha, čas a hmotnosť a iste ste si všimli, aj
aká je hustota materiálu, z ktorého sú vyrobené jednotlivé telesá.
Applet
zobrazuje okrem jednotkových vektorov v smeroch jednotlivých osí aj
vektory okamžitej uhlovej rýchlosti a momentu hybnosti.
Zistite, v akej mierke sú v applete zobrazené, konkrétne koľko rad/s
a koľko kg.dm2.s–1 pripadá na jednotku
dĺžky na zobrazovacej ploche.
[Návod: Vyberte si
vhodné teleso, napríklad disk a vhodné začiatočné podmienky pre
simuláciu. Meraním času vypočítajte veľkosť uhlovej rýchlosti.
Použite vhodnú projekciu a zistite dĺžku vektora
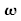 .
Z toho určte mierku pre uhlovú rýchlosť. Mierku pre moment hybnosti
určte podobne. Využite pri tom to, že môžete vyrátať, aký je
moment hybnosti disku ak obieha známou uhlovou rýchlosťou a vy
poznáte jeho hustotu a jeho rozmery dokážete v applete určiť.] .
Z toho určte mierku pre uhlovú rýchlosť. Mierku pre moment hybnosti
určte podobne. Využite pri tom to, že môžete vyrátať, aký je
moment hybnosti disku ak obieha známou uhlovou rýchlosťou a vy
poznáte jeho hustotu a jeho rozmery dokážete v applete určiť.]
Späť na applet ...
|
|
Bádanie 5 - Stopy
nás privádzajú k podstate.
Nastavte
applet tak, aby v sústave laboratória zobrazoval disk a
zároveň aby zobrazoval osi sústavy spojenej s tuhým telesom a tiež
stopy týchto vektorov. Nastavte potom nasledujúce začiatočné
podmienky simulácie:
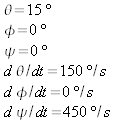
- Predtým,
ako spustíte simuláciu, odhadnite, po akých krivkách sa budú
pohybovať konce vektorov
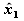 , ,
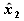 a
a
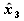 .
Spustite simuláciu. Aký tvar má stopa konca vektora .
Spustite simuláciu. Aký tvar má stopa konca vektora
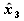 ?
Dalo sa to očakávať? Aký tvar majú stopy koncov vektorov ?
Dalo sa to očakávať? Aký tvar majú stopy koncov vektorov
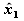 a
a
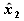 ?
Sú to uzavreté krivky? Vykonáva disk kolísanie, ktoré sa dá považovať
za malé? ?
Sú to uzavreté krivky? Vykonáva disk kolísanie, ktoré sa dá považovať
za malé?
- Stlačte RESET a nastavte iné počiatočné podmienky:
Predtým, ako spustíte simuláciu, odhadnite, či sa bude disk
kolísať viac, alebo menej. Spustite simuláciu a sledujte pohyb
vektorov
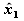 a
a
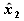 .
Po akých krivkách sa pohybujú ich konce? Sú tieto krivky uzavreté
(aspoň približne)? Vykonáva teraz disk kolísanie, ktoré sa dá
považovať za malé? .
Po akých krivkách sa pohybujú ich konce? Sú tieto krivky uzavreté
(aspoň približne)? Vykonáva teraz disk kolísanie, ktoré sa dá
považovať za malé?
- Overte
vyskúšaním niekoľkých ďalších začiatočných podmienok, či sa vektory
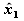 a
a
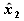 správajú podobne vždy, keď tanier vykonáva malé kolísanie!
správajú podobne vždy, keď tanier vykonáva malé kolísanie!
- Nastavte
začiatočné podmienky
Krokujte simuláciu pokým koniec vektora
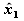 nevykoná polovicu obehu po svojej kružnici. Sledujte pritom
ako sa správa vektor
nevykoná polovicu obehu po svojej kružnici. Sledujte pritom
ako sa správa vektor
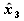 .
Akú časť svojej kružnice obehne jeho koniec? Zmeny smeru vektora .
Akú časť svojej kružnice obehne jeho koniec? Zmeny smeru vektora
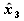 súvisa s kolísaním disku. Aký záver sa dá teraz urobiť o pomere
frekvencií kolísania a otáčania disku?
súvisa s kolísaním disku. Aký záver sa dá teraz urobiť o pomere
frekvencií kolísania a otáčania disku?
- Ak chcete vedieť, prečo
sa pri malom kolísaní konce vektorov musia
pohybovať tak, ako ste to videli pred chvíľou, prečítajte si Kapitolu
4, Jednoduchší spôsob,
z učebného textu.
Späť na applet ...
|
|
Bádanie 6 - Jestvuje niečo, čo sa musí otočiť najmenej dvakrát aby sa to
dostalo do pôvodného stavu?
Nastavte applet tak, aby v sústave laboratória zobrazoval pravidelný
štvorboký hranol a zároveň aby zobrazoval osi sústavy spojenej s
tuhým telesom a tiež stopy týchto vektorov. Nastavte potom
nasledujúce začiatočné podmienky simulácie:
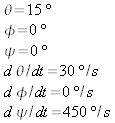
- Predtým, ako spustíte simuláciu, si spomeňte na hodnotu
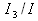 ,
získanú v Bádaní 2 pre pravidelný štvorboký hranol. K akému pomeru
frekvencií chvenia a otáčania by to malo viesť pre malé chvenie?
Odhadnite, po akých
krivkách sa budú pohybovať konce vektorov ,
získanú v Bádaní 2 pre pravidelný štvorboký hranol. K akému pomeru
frekvencií chvenia a otáčania by to malo viesť pre malé chvenie?
Odhadnite, po akých
krivkách sa budú pohybovať konce vektorov
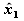 , ,
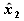 a
a
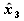 !
Spustite simuláciu a overte, či bol váš odhad správny. Sú krivky
uzavreté? Dá sa pohyb považovať za malé kolísanie? !
Spustite simuláciu a overte, či bol váš odhad správny. Sú krivky
uzavreté? Dá sa pohyb považovať za malé kolísanie?
- Koľkokrát sa musí os
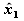 hranola
otočiť dookola, aby vykonal koniec vektora hranola
otočiť dookola, aby vykonal koniec vektora
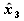 jednu otáčku po svojej kružnici? Koľkokrát sa teda musí hranol
otočiť, aby sa dostal do pôvodného stavu?
jednu otáčku po svojej kružnici? Koľkokrát sa teda musí hranol
otočiť, aby sa dostal do pôvodného stavu?
- Špekulatívna otázka: V kvantovej mechanike má objekt so spinom
½ (elektrón) podobné vlastnosti. Ak otáčame prístrojom, ktorým
ho pozorujeme, musíme ním otočiť až o 720°, aby sa stavový vektor
spinu rovnal pôvodnému stavovému vektoru. Je tu podobnosť s
telesami, pre ktoré
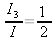 ? ?
Späť na applet ...
|
|