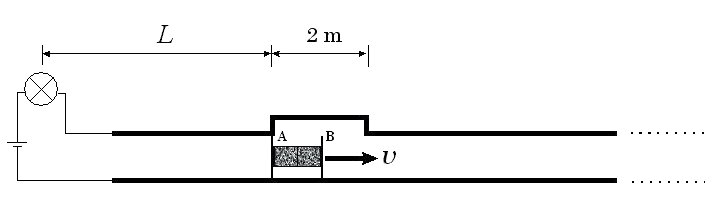
Let us consider two long parallel conducting rails that are open at one end but connected at the other end through a bulb and a source of steady voltage all in series (Fig. 1). One of the rails has a gap of rest length 2 meters that is bridged by a parallel conducting strip very close to the rail itself. An H-shaped object with conducting prongs A and B connected by an insulating rod fits snugly between the guide rails and is capable of moving freely between them like a shuttle in a weaver's loom. The rest length of the shuttle is also equal to 2 meters.
 |
| Fig.1. Configuration of the circuit in the rail frame. |
When both prongs of the shuttle are to the left of the gap (see Fig. 1), the rails are shorted by the shuttle and the bulb glows. We wish to examine from the "rail frame" and the "shuttle frame" what happens to the glowing bulb if the shuttle moves forward uniformly at a speed v with respect to the rails. We assume that the friction and electrical interaction are small enough that the momentum of the shuttle changes by a negligible amount during its motion.
When observed from the rail frame the moving shuttle AB suffers a length contraction and occupies the position shown in Fig. 1 at the instant at which A is losing contact with the upper rail. Thereafter, there occurs a period of time during which both prongs A and B lose contact with the upper rail and the circuit opens. The bulb should therefore stop glowing until prong B of the shuttle reestablishes contact with the rail and the circuit closes again. Thus in the rail frame the bulb switches off for a time Toff before starting to glow again.
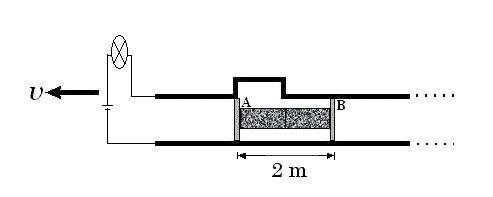 |
| Fig.2. Configuration of the circuit in the shuttle frame. |
When observed from the shuttle frame, the bulb and the entire circuit move backwards and it is the gap and the bridge across it that suffer the length contraction (see Fig. 2 ). Since the shuttle is now longer than the gap, there is no instant at which both prongs A and B of the shuttle lie within the gap. Therefore, one or the other of the prongs A and B is always in contact with the rails since the upper rail establishes contact with B before it loses contact with A. Hence, in the shuttle frame, the circuit never becomes open. It then appears that the bulb should never stop glowing, which conclusion is paradoxical.
You should decide: Does the bulb flicker, or not? The Java program bellow will help you decide.
The applet will show you the animation of the shuttle and the rails from two different frames. You can choose the frame by selecting the laboratory frame or the rocket frame in the combo box in the lower right of the display. The laboratory frame corresponds to the rails frame, while the rocket corresponds to the rest frame of the shuttle.
You can measure positions of events in the animation by placing the mouse cursor above any desired point. Its position is displayed in the lower left of the display. Position is measured in meters.
Time of any event is displayed in the upper left of the display. Time is measured in meters of light travel time. You can use the Step Back and Step Forward buttons to step the animation so as to measure the time more precisely.
Drag the display with your mouse when you want to move it horizontally. For instance, try dragging the initial display in the laboratory frame to the right and you will see the light bulb.
You can change the relative velocity of the shuttle and the rails using the velocity text field. After typing in the desired value it is required to press the Reset button.
Essential for resolving this paradox is to understand that the light bulb doesn't respond immediatelly to what is going on in the gap area. The only way for the bulb to "see" what is going on there is to wait for the electomagnetic signals to reach it. Below we will suppose that these signals travel at the speed of light.
Exploration 1: Observing within the laboratory frame
Set the frame to the laboratory and the velocity to 0.866 if you have played with the applet. Press START button and observe the animation. You will see four events in the gap area and the corresponding information signals originated there. See what is the effect those four traveling signals have on the light bulb. (You can move the display horizontally by dragging it with the mouse). Does it flicker in the laboratory frame?
Exploration 2: Taking data within the laboratory frame
Construct a table in which you will record times and positions of the following four events: (1) Prong B looses contact with the upper rail, (2) Prong A looses contact with the upper rail, (3) Prong B reestablishes contact with the upper rail, (4) Prong A reestablishes contact with the upper rail.
Now construct another table with the times and positions of the following four events: (a) Signal "disconnected at B" reaches the bulb, (b) Signal "disconnected at A" reaches the bulb, (c) Signal "connected at B" reaches the bulb, (d) Signal "connected at A" reaches the bulb. Be sure to put the events in your table in the time increasing order. What is the order of those events? Is it reasonable that the bulb flickers? What is the time Toff, the bulb is totally dark in the laboratory frame?
Exploration 3: Observing within the rocket frame
Set the frame to the rocket and the velocity to 0.866 if you have played with the applet. Press START button and observe the animation. You will see four events in the gap area and the corresponding information signals originated there. See what is the effect those four traveling signals have on the light bulb. (You can move the display horizontally by dragging it with the mouse). Please, be patient till the signals reach the bulb! Does the bulb flicker in the rocket frame?
Exploration 4: Taking data within the rocket frame
Construct a table in which you will record times and positions of the following four events: (1) Prong B looses contact with the upper rail, (2) Prong A looses contact with the upper rail, (3) Prong B reestablishes contact with the upper rail, (4) Prong A reestablishes contact with the upper rail.
Now construct another table with the times and positions of the following four events: (a) Signal "disconnected at B" reaches the bulb, (b) Signal "disconnected at A" reaches the bulb, (c) Signal "connected at B" reaches the bulb, (d) Signal "connected at A" reaches the bulb. Be sure to put the events in your table in the time increasing order. What is the order of those events? Is it reasonable that the bulb flickers? What is the time T'off, the bulb is totally dark in the rocket frame? Is this what you would expect considering the time dilation formula?
Exploration 5: Do your measurments comply with the Lorentz trasformation?
In Explorations 2 and 4 you have constructed the tables of times and positions of the same events (1), (2), (3), (4), (a), (b), (c), and (d) as observed in two different frames. Show that those two tables are consistent regarding the Lorentz transformation!
Exploration 6: Time to predict!
Now it's time to test your prediction power! Imagine the velocity of the shuttle with respect to the rails is v=0.5. Work generally (using general formulas). Use numbers only at the end to get the numerical results! Predict the times and positions of the following four events in the Laboratory frame: (1) Prong B looses contact with the upper rail, (2) Prong A looses contact with the upper rail, (3) Prong B reestablishes contact with the upper rail, (4) Prong A reestablishes contact with the upper rail. Construct a table for your predictions similar to that in Exploration 2.
Predict the times and positions of the another four events in the Laboratory frame: (a) Signal "disconnected at B" reaches the bulb, (b) Signal "disconnected at A" reaches the bulb, (c) Signal "connected at B" reaches the bulb, (d) Signal "connected at A" reaches the bulb. Construct a table for your predictions similar to that in Exploration 2.
Find the general expression for time Toff in terms of v and other relevant quantities.
Now use the applet and see if your predictions were correct!
Now switch to the rocket frame and predict times and positions of the four events: (1) Prong B looses contact with the upper rail, (2) Prong A looses contact with the upper rail, (3) Prong B reestablishes contact with the upper rail, (4) Prong A reestablishes contact with the upper rail. Construct a table for your predictions similar to that in Exploration 4.
Predict the times and positions of the another four events in the Rocket frame: (a) Signal "disconnected at B" reaches the bulb, (b) Signal "disconnected at A" reaches the bulb, (c) Signal "connected at B" reaches the bulb, (d) Signal "connected at A" reaches the bulb. Construct a table for your predictions similar to that in Exploration 4.
Find the general expression for time T'off as measured in the rocket frame in terms of v and other relevant quantities.
Now use the applet and see if your predictions were correct!
Edwin F. Taylor, John A. Wheeler: Spacetime Physics - Introduction to Special Relativity, 2-nd Edition, W. H. Freeman &Co., New York, 1992
G.P.Sastry, Is Length Contraction Really Paradoxical?, American Journal of Physics, Vol 55, October 1987
The source code of this applet is published here under the GNU GPL licence without any guarantee. For the details, please see the text of the licence.
Written by Slavomir Tuleja, November 2003.