We all are 3 dimensional beings and don't have any experience with 4 dimensional world. In this interactive document you will have a chance to get an experience from the 4-cube also called hypercube.
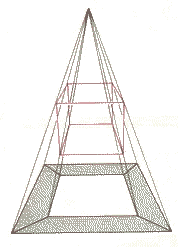
How can we see a hypercube? By means of projection. We will try to explain this by analogy. If we want to make an image of an ordinary 3-cube, we can project all its vertices and edges by imaginary light beams to a plane (see the image below).

By looking at the projection we know what the projected object looks like. The smaller square represents the farthest face while the largest square represents the front face of the cube.
Similarly we can project a 4-cube to the 3 dimensional analogue of a plane. What we get is a 3 dimensional image of a 4-cube.
The applet below shows an image of a 4-cube projected on hyperplane x4=0. The 4-cube is in special position. Its edges are lined up with the x1, x2, x3, and x4 axes directions. Edges in x1 direction are drawn in RED color, those in x2 direction in GREEN, those in x3 direction in BLUE and finally, those in x4 direction in YELLOW. Arrows represent positive directions.
Analogically to a 2-d projection of 3-cube, the 3-d projection of 4-cube consists of 3-cubes or deformed 3-cubes, representing the 3-d faces of 4-cube. There are 8 of them. The one farthest away in x4 direction from the projection center is represented by a small cube inside the bigger one, which represents the one closest to the projection center. The 4-cube has 16 vertices, 8 3-d faces and 32 edges.
Now it's time to rotate the hypercube! Rotate how? In any of six possible rotation planes: x1-x2, x1-x3, x1-x4, x2-x3, x2-x4, x3-x4. Rotation in each of these possible planes is measured by a coresponding angle. For instance, rotation in x1-x2 plane is given by the angle alpha12, etc.
The applet allows you to observe the effect of these rotations on the shape of the 3-d image of the hypercube. Please, investigate each rotation alone and let all the other angles equal to zero. Only after doing this you should try to combine the rotations to get a general rotation. Some rotations lead to intuitive results, some are surprising. Have fun!
The applet above uses Open Source Physics library developed by Dr. Wolfgang Christian et. al. at Davidson College. It's source code is published here under the GNU GPL licence without any guarantee. For the details, please see the text of the licence.
Written by Slavomir Tuleja, August 2003.